Параллелограмм – это четырехугольник, у которого противоположные стороны параллельны и равны между собой. Но что происходит с его смежными сторонами? Они также параллельны или могут пересекаться?
Для ответа на этот вопрос нам необходимо разобраться в свойствах параллелограмма. За помощью обратимся к определению понятия "смежные стороны".
Смежные стороны – это стороны, которые имеют общую вершину. В параллелограмме это означает, что смежные стороны имеют общую точку, где они пересекаются. Однако, они не пересекают друг друга и остаются параллельными.
Таким образом, смежные стороны параллелограмма параллельны и не пересекаются. Это является одним из основных свойств параллелограмма и отличает его от других четырехугольников.
Различия между параллелограммами и другими фигурами
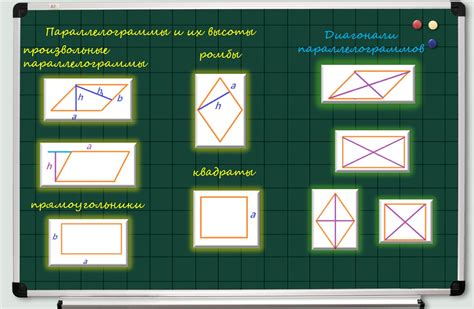
1. Стороны параллелограмма. В параллелограмме противоположные стороны параллельны и равны по длине, в отличие от других фигур, где стороны могут быть разнообразными.
2. Углы параллелограмма. Углы параллелограмма очень важны, так как они являются смежными и сумма смежных углов всегда равна 180 градусам. В других фигурах, углы могут иметь разные значения.
3. Диагонали параллелограмма. В параллелограмме, диагонали делятся пополам и пересекаются под прямым углом, в отличие от других фигур, где диагонали могут быть разнонаправленными и пересекаться не под прямым углом.
4. Свойства параллелограмма. Параллелограмм обладает рядом уникальных свойств, которые его отличают от других фигур. Он имеет равные противоположные стороны, равные противоположные углы и диагонали, пересекающиеся под прямым углом. Другие фигуры не обязательно обладают такими свойствами.
Итак, параллелограмм - это особая фигура, которая имеет уникальные характеристики и отличается от других фигур по многим параметрам.
Параллелограммы: определение и свойства
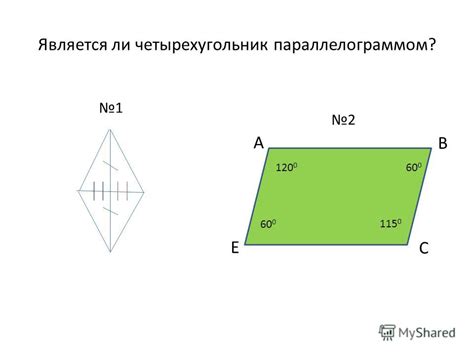
Свойства параллелограмма:
1. Противоположные стороны параллельны: В параллелограмме две противоположные стороны всегда параллельны. Это означает, что их направления совпадают и они никогда не пересекаются.
2. Противоположные стороны равны: В параллелограмме две противоположные стороны всегда равны друг другу. Это означает, что их длины одинаковы.
3. Противоположные углы равны: В параллелограмме два противоположных угла всегда равны друг другу. Это означает, что их величины одинаковы.
4. Соседние углы дополнительны: В параллелограмме два соседних угла всегда дополняют друг друга до 180 градусов. Это означает, что их сумма равна 180 градусов.
5. Диагонали делятся пополам: В параллелограмме диагонали, соединяющие противоположные вершины, делятся пополам. Это означает, что каждая диагональ делит параллелограмм на две равные по площади части.
6. Сумма углов параллелограмма равна 360 градусов: В параллелограмме сумма всех его углов всегда равна 360 градусов.
Таким образом, параллелограммы обладают рядом характерных свойств, которые делают их отлично определяемыми и выделяющимися среди других четырехугольников.
Зависимость между сторонами и углами параллелограмма
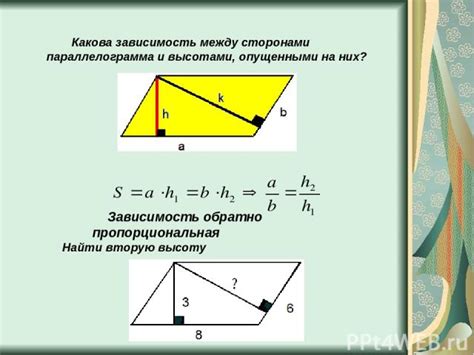
В параллелограмме смежные стороны параллельны и равны друг другу. Это означает, что если одну из сторон параллелограмма обозначить как а, то смежная сторона также будет равна а. Также стороны параллелограмма делят его диагонали пополам.
Углы параллелограмма имеют свойство суммироваться до 180 градусов. То есть если у параллелограмма один угол равен х градусов, то противоположный угол будет также равен х градусов. Кроме того, дополнительные углы (угол между смежными сторонами и дополнительный угол с противоположной стороной) также будут равны.
С учетом этих свойств, можно установить зависимость между сторонами и углами параллелограмма. Если известны углы параллелограмма, то можно определить длины его сторон, и наоборот.
Например, если известны длины двух смежных сторон параллелограмма, можно найти углы с помощью соответствующих тригонометрических функций, например тангенса. При этом угол между смежными сторонами противоположен дополнительному углу с противоположной стороной.
Таким образом, между сторонами и углами параллелограмма существует определенная зависимость, которую можно использовать для решения различных задач и заданий связанных с этой фигурой.
Параллельность смежных сторон в параллелограмме
Смежные стороны параллелограмма называются такими, которые имеют общий конец и не являются противоположными. Согласно свойствам параллелограмма, смежные стороны всегда параллельны друг другу.
Это справедливо для любого параллелограмма, независимо от его размеров и формы. Если взять любые две смежные стороны параллелограмма и провести к ним соответствующие перпендикуляры, то получатся две прямые, которые будут параллельны.
Параллельность смежных сторон параллелограмма позволяет рассматривать его как геометрическую фигуру с двумя параллельными сторонами и двумя парами равных углов. Это свойство используется при решении задач на нахождение периметра и площади параллелограмма, а также при построении и анализе различных геометрических фигур.
| Свойства параллелограмма: | Доказательство: |
|---|---|
| Противоположные стороны равны | Диагонали параллелограмма делятся пополам |
| Противоположные углы равны | Параллельность смежных сторон и перпендикулярность диагоналей |
| Диагонали параллельны | Перпендикулярность диагоналей |
Взаимное расположение смежных сторон в параллелограмме
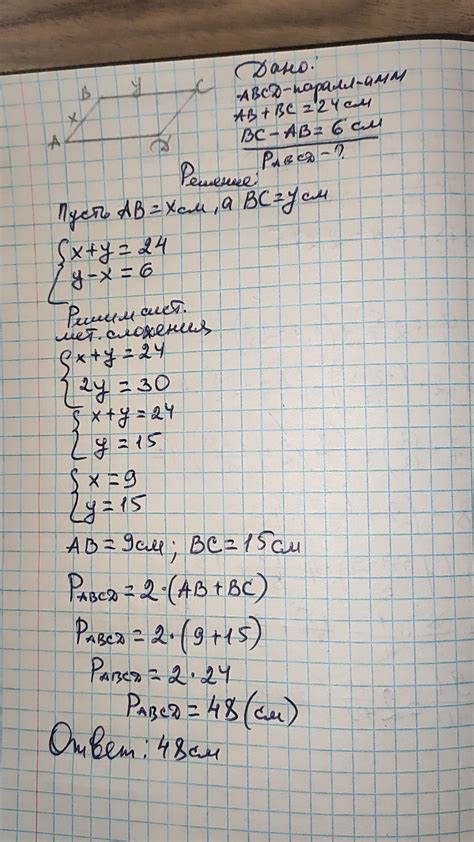
В параллелограмме смежные стороны называются так, потому что они имеют общую вершину и лежат на одной прямой, но при этом не пересекаются. Это делает их особенно важными для изучения этой фигуры.
Смежные стороны параллелограмма всегда параллельны и равны между собой. Такой результат следует из свойств параллелограмма: противоположные стороны параллельны и равны.
Если мы знаем, что смежные стороны параллелограмма пересекаются или не параллельны, то это может служить признаком, что данная фигура не является параллелограммом. Например, если две смежные стороны пересекаются, то мы имеем дело скорее с трапецией или другим типом четырехугольника.
Взаимное расположение смежных сторон в параллелограмме не только определяет геометрические свойства фигуры, но и позволяет решать задачи на построение и измерения.
Примеры параллелограммов в природе и архитектуре

- Волна на океане. Волны на поверхности моря имеют форму параллелограмма, где вершины соединены линиями, а стороны параллельны и одинаковой длины.
- Горные хребты. Вид сверху на горные хребты также образует параллелограмм, где вершины представлены горными вершинами, а стороны соединены германием гор.
- Постройки архитектурных зданий. Большинство зданий, особенно высотных, имеют параллелограмматическую форму плана: противоположные стороны параллельны, а углы прямые.
- Движение автомобиля. Казалось бы, движущийся автомобиль не похож на параллелограмм. Однако, если просмотреть его путь с определенного ракурса, например, из вертолета или с высокого здания, то будет видно, что автомобиль следует по линиям параллелограмма.
- Схема пролета мостовой. Проезжая по мосту, можно увидеть, что форма его мостовой напоминает параллелограмм, где стороны моста параллельны, а опоры заменяют вершины.
Это лишь некоторые примеры параллелограммов, которые встречаются в природе и архитектуре. Изучение их формы и свойств помогает лучше понять и описать окружающий нас мир.
Пересечение смежных сторон в параллелограмме

Если смежные стороны параллелограмма не пересекаются, то они параллельны друг другу. Это означает, что углы между этими сторонами равны и соседние углы параллелограмма также равны.
Однако, смежные стороны параллелограмма могут быть и пересекающимися. В этом случае углы между сторонами уже не будут равными, а соседние углы могут быть различными. При таком пересечении смежных сторон параллелограмма также возникают дополнительные свойства и взаимосвязи между углами и сторонами.
Различные комбинации пересечений смежных сторон параллелограмма создают разнообразные типы параллелограммов, такие как ромб, квадрат, прямоугольник и трапеция. Каждый из этих типов имеет свои характеристики и свойства.
Важно отметить, что параллелограмм - это частный случай трапеции, у которой две пары параллельных сторон. Таким образом, в трапеции также возможно пересечение смежных сторон, но углы и свойства трапеции будут отличаться от параллелограмма.
Сравнение параллелограмма с другими четырехугольниками
В отличие от обычных четырехугольников, все стороны параллелограмма параллельны и равны друг другу. Кроме того, его противоположные углы также равны.
Однако, параллелограмм отличается от других четырехугольников, таких как прямоугольник, ромб или квадрат.
Прямоугольник имеет все углы прямые, но стороны могут быть разной длины.
Ромб имеет все стороны равными, но углы не обязательно прямые.
Квадрат, в свою очередь, является и параллелограммом, и прямоугольником, и ромбом. Все его свойства сочетаются в одной фигуре.
Таким образом, параллелограмм является уникальным геометрическим объектом, который может быть отличен по своим характеристикам от других четырехугольников.