В начертательной геометрии одним из ключевых аспектов является исследование соотношений между прямыми и плоскостями. Знание законов и классификации этих соотношений необходимо для построения точных и ясных графических представлений различных объектов и конструкций. Понимание этих законов поможет студентам геометрии развить навыки визуализации и анализа пространственных отношений.
Одним из основных законов, регулирующих взаимное расположение прямых и плоскостей, является закон пересечения. Согласно этому закону, каждая прямая пересекает каждую плоскость в единственной точке, если эта точка не лежит на прямой и не является пересечением двух или более прямых. Таким образом, пересечение прямой и плоскости может быть представлено как точка.
Кроме того, в начертательной геометрии существуют и другие законы, например, закон параллельности и закон секущих. Закон параллельности утверждает, что если две прямые параллельны одной плоскости, то они параллельны и другим плоскостям, параллельным данной. Закон секущих гласит, что если две прямые пересекаются в одной плоскости, то они пересекаются и в каждой другой плоскости, проходящей через обе прямые.
Классификация соотношений прямых и плоскостей в начертательной геометрии основана на их взаимном расположении и взаимодействии. Прямые могут быть параллельными, пересекающимися или совпадающими. Плоскости могут быть параллельными, пересекающимися или совпадающими. Эта классификация важна для построения точных и понятных графических представлений и для решений различных геометрических задач.
Определение и свойства прямых и плоскостей
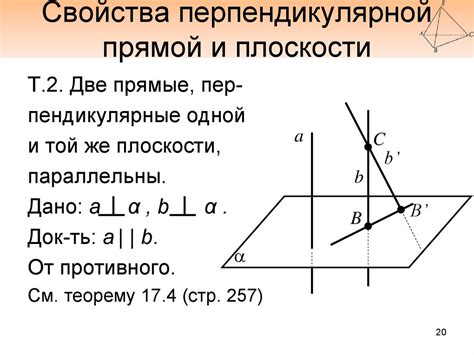
Свойства прямых:
- Прямая проходит через любые две точки, лежащие на ней.
- Если две прямые пересекаются в одной точке, то они называются скрещивающимися.
- Если две прямые не пересекаются и лежат в одной плоскости, они называются параллельными.
- Сумма углов, образованных прямыми при пересечении, равна 180 градусам. Это называется прямым углом.
Плоскость – это геометрическое место всех точек, которые можно получить движением прямой в любом направлении. Она не имеет конца и простирается в бесконечность по всем направлениям.
Свойства плоскостей:
- Плоскость проходит через любые три точки, которые не лежат на одной прямой.
- Две плоскости могут пересекаться по прямой линии. Такие плоскости называются скрещивающимися.
- Параллельные плоскости никогда не пересекаются и всегда имеют одинаковое расстояние между собой.
- Три пересекающиеся плоскости могут образовывать сонаправленные ребра.
Классификация прямых в пространстве
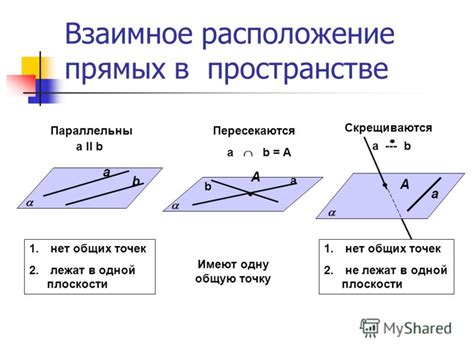
В пространстве существует несколько способов классифицировать прямые, в зависимости от их положения и взаимного расположения.
- Скрещивающиеся прямые: прямые, которые пересекаются и не лежат в одной плоскости.
- Секущие прямые: прямые, которые пересекаются и лежат в одной плоскости.
- Параллельные прямые: прямые, которые не пересекаются и не лежат в одной плоскости.
- Пересекающаяся прямая: прямая, которая пересекает другую прямую и лежит в одной плоскости с ней.
Также прямые могут быть расположены по отношению к плоскостям:
- Скользящая прямая: прямая, которая пересекает все плоскости параллельно заданной.
- Наклонная прямая: прямая, которая пересекает все плоскости наклонно.
- Плоскость сечения: плоскость, которая пересекает прямую и образует на ней сечение.
Знание классификации прямых позволяет более точно определить их положение в пространстве и проводить анализ их взаимного расположения.
Законы соотношений прямых и плоскостей
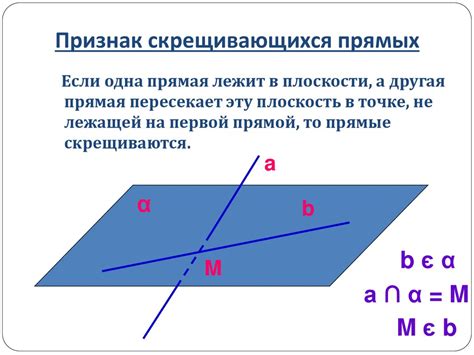
В начертательной геометрии существуют определенные законы, которые помогают определить соотношения между прямыми и плоскостями. Знание этих законов позволяет проводить точные расчеты и строить сложные конструкции.
Один из основных законов – закон параллельности. Согласно этому закону, если прямая пересекает одну плоскость, параллельную другой плоскости, то эти две плоскости также параллельны между собой. Этот закон помогает строить параллельные прямые и плоскости и применяется в различных инженерных и архитектурных задачах.
Другой важный закон – закон перпендикулярности. Согласно этому закону, если прямая пересекает одну плоскость перпендикулярно и другую плоскость перпендикулярно, то эти две плоскости перпендикулярны между собой. Этот закон используется при построении перпендикулярных линий и плоскостей, например, при создании прямоугольных конструкций.
Также существует закон секущей. Согласно этому закону, если прямая пересекает одну плоскость, параллельную другой плоскости, то эти две плоскости разделяют прямую на отрезки, пропорциональные расстоянию от точки пересечения до каждой из плоскостей. Этот закон применяется для определения пропорций и отношений в трехмерных моделях и проекциях.
Знание законов соотношений прямых и плоскостей в начертательной геометрии является необходимым для точных и аккуратных конструкций. Они помогают определить геометрические свойства объектов и правильно строить сложные формы. При изучении этих законов важно понимать их применение в реальных задачах и приводить соответствующие примеры.
Применение начертательной геометрии в решении задач
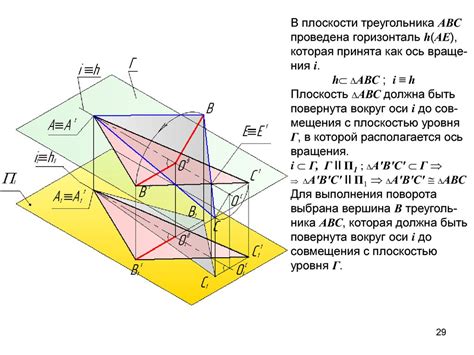
Одной из основных задач начертательной геометрии является определение взаимного расположения двух прямых или плоскостей. Эта задача часто возникает при решении задач на пересечение прямых и плоскостей, построение параллельных и перпендикулярных прямых, а также при определении углов между прямыми и плоскостями.
Для решения этих задач в начертательной геометрии существует ряд законов и классификаций соотношений между прямыми и плоскостями. Например, закон параллельности утверждает, что если две прямые расположены одновременно параллельно третьей прямой, то они также параллельны друг другу.
Также в начертательной геометрии существует классификация пересечения прямых. В зависимости от их взаимного положения, прямые могут пересекаться, быть параллельными или совпадать.
Кроме того, начертательная геометрия позволяет строить и анализировать различные фигуры, такие как треугольники, прямоугольники, круги и много других. С помощью начертательной геометрии можно измерять длины отрезков, углы и площади фигур.
Все эти принципы и методы начертательной геометрии составляют основу для решения различных задач в различных областях, таких как архитектура, инженерия, физика и география. Умение анализировать и визуализировать пространственные объекты позволяет решать сложные геометрические задачи и улучшать качество проектов и исследований.