Определение вершин многоугольника является важной задачей, которая имеет множество практических применений. Например, задача построения оптимального плана размещения объектов на плоскости требует определения формы многоугольника, в котором будут размещены объекты.
Метод определения вершин многоугольника с минимальными усилиями основан на алгоритме, который позволяет найти наименьшую овещающую многоугольник для заданного набора точек на плоскости. Овещающий многоугольник – это многоугольник, все точки которого лежат вне заданного множества точек, но в то же время содержащий все эти точки внутри себя. Такой многоугольник может быть невыпуклым и иметь произвольную форму.
Метод определения вершин многоугольника с минимальными усилиями состоит из следующих шагов: сначала необходимо отсортировать заданные точки по их полярному углу относительно стартовой точки. Затем алгоритм последовательно строит овещающий многоугольник, добавляя каждую следующую точку в многоугольник так, чтобы она была видимой из текущей точки многоугольника. В результате работы алгоритма получается искомый минимальный многоугольник.
Определение вершин многоугольника
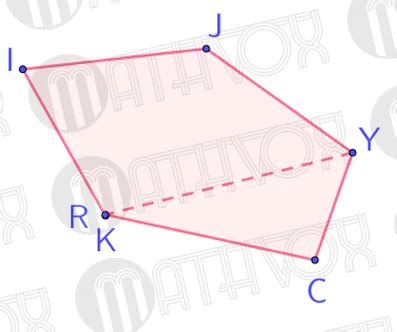
Существует несколько методов определения вершин многоугольника, включая метод перебора всех возможных комбинаций, метод использования угловых точек и метод пользования алгоритма Грэхема.
- Метод перебора всех возможных комбинаций заключается в проверке всех возможных пар сторон многоугольника. Если найдется пересечение, то точка пересечения является вершиной многоугольника.
- Метод использования угловых точек основан на выявлении угловых точек многоугольника, то есть точек, в которых он поворачивает. Угловые точки могут быть найдены, например, путем проверки знаков угловых поворотов.
- Метод пользования алгоритма Грэхема базируется на сортировке точек многоугольника по углу относительно заданной точки-начала. Затем, используя стек, можно определить вершины многоугольника.
Выбор конкретного метода определения вершин многоугольника зависит от его особенностей и требований задачи.
Способы определения

Существует несколько способов определения вершин многоугольника с минимальными усилиями. Некоторые из них основаны на математических моделях и алгоритмах, другие используют технические средства и инструменты.
Вот некоторые из наиболее распространенных способов определения вершин многоугольника:
- Визуальный метод: с помощью глаз и руки можно определить вершины многоугольника, проводя контур фигуры или измеряя углы.
- Математический метод: с использованием геометрических формул и алгоритмов можно точно определить координаты вершин, используя известные параметры многоугольника.
- Использование специализированных инструментов: существуют специальные инструменты, такие как геодезические приборы или лазерные измерители, которые позволяют определить координаты вершин с высокой точностью.
- Анализ изображений: с помощью компьютерного зрения и алгоритмов обработки изображений можно автоматически определить вершины многоугольника на фотографии или видео.
Каждый из этих способов имеет свои преимущества и ограничения, и выбор метода зависит от конкретной ситуации и требуемой точности определения вершин многоугольника.
Применение видеотехнологий

Видеотехнологии активно применяются в методе определения вершин многоугольника с минимальными усилиями. Они позволяют производить быструю и точную обработку полученных данных, а также упрощают процесс определения вершин.
Одним из способов применения видеотехнологий в данном методе является использование видеокамеры для записи процесса перемещения вершины многоугольника. Затем полученный видеофайл можно анализировать с помощью специальных программ, которые определяют координаты вершин на каждом кадре. Такой подход позволяет обработать большое количество данных за короткое время и получить достоверные результаты.
Кроме того, видеотехнологии позволяют визуализировать процесс определения вершин многоугольника. С помощью видеозаписи можно показать каждый шаг алгоритма и проиллюстрировать основные принципы работы метода. Это упрощает понимание процесса и помогает пользователю быстро освоиться с методом определения вершин.
Видеотехнологии также позволяют производить дополнительные измерения и анализ данных. Например, с их помощью можно определить время работы алгоритма на каждой итерации или оценить точность полученных результатов. Такие данные полезны для дальнейшей оптимизации метода и повышения его точности.
Таким образом, применение видеотехнологий в методе определения вершин многоугольника с минимальными усилиями является эффективным и полезным. Они ускоряют и упрощают процесс определения вершин, облегчают понимание и изучение метода, а также позволяют проводить дополнительные анализы и измерения.
Роль компьютерного зрения
Одним из важных аспектов компьютерного зрения является способность компьютера распознавать и анализировать объекты на изображениях. Это может быть полезно, например, для определения границ объектов, распознавания лиц, идентификации предметов или обнаружения нежелательных объектов.
Компьютерное зрение также играет важную роль в разработке алгоритмов, которые позволяют компьютеру автоматически определять вершины многоугольника с минимальными усилиями. Путем анализа изображений и применения специальных алгоритмов компьютер может определить положение и форму многоугольника, что помогает упростить и автоматизировать процесс исследования и проектирования различных продуктов и систем.
Таким образом, компьютерное зрение имеет огромный потенциал во многих сферах деятельности, и его развитие продолжается. Современные технологии и алгоритмы компьютерного зрения позволяют компьютерам анализировать и обрабатывать изображения и видео с высокой точностью и скоростью, что делает их незаменимыми инструментами во многих областях, где требуется высокая точность и скорость обработки информации.
Методы с минимальными усилиями

Один из методов, который широко используется для определения вершин многоугольника с минимальными усилиями, - алгоритм Грэхема. Он основан на идее сортировки точек многоугольника в порядке возрастания угла, который образуют они с некоторой фиксированной точкой, называемой начальной точкой. После сортировки точки соединяются линиями в порядке их следования, образуя многоугольник.
Еще одним методом является метод заметающей прямой. Он основан на идее проложить прямую линию через область, в которой находятся точки многоугольника, с последующим построением пересечений этой линии со всеми точками многоугольника. Таким образом получается множество пересечений, которые можно рассматривать как вершины многоугольника.
При использовании методов с минимальными усилиями для определения вершин многоугольника необходимо учитывать условия задачи и особенности точек, поскольку они могут влиять на алгоритмы и результаты. Кроме того, определение вершин многоугольника с минимальными усилиями может быть связано с математическими вычислениями и анализом данных, которые требуют высокой точности и аккуратности.
В целом, методы с минимальными усилиями являются мощными инструментами, которые позволяют оптимизировать процессы и сэкономить ресурсы при определении вершин многоугольника. Они предоставляют возможность улучшить эффективность и точность выполнения задач, что делает их незаменимыми во многих областях науки и техники.