Деление является одной из основных операций в математике. Оно позволяет нам разделить целое число на другое число и определить результат этой операции. Однако зачастую деление не дает нам частного без остатка, а дает нам десятичную дробь. Но что если мы хотим найти только целую часть? В этой статье мы рассмотрим различные способы нахождения целой и дробной частей при делении.
Первый способ - это простое деление в столбик. Для этого мы записываем делимое число и делитель в столбик и начинаем делить как обычно. При этом, если в результате выполняется деление без остатка, полученное частное является целой частью. Если же остаток присутствует, мы записываем его ниже и дальше выполняем деление только остатка на делитель, чтобы найти дробную часть.
Еще один способ - это использование функции целочисленного деления. В некоторых программных языках, таких как Python, С++ или Java, существует оператор "div", который позволяет нам найти целую часть при делении без остатка. Это очень удобно, так как нам не нужно выполнять дополнительные шаги для нахождения целой части. Просто записываем операцию "делимое div делитель" и получаем результат.
Также стоит упомянуть способ, использующий операцию "деление нацело". В языке программирования С, к примеру, существует оператор "%", который позволяет найти остаток от деления двух чисел. Если имеется выражение "делимое % делитель", то остаток от деления будет равен дробной части. Чтобы найти целую часть, мы можем использовать операцию "деление с округлением вниз", например, функцию floor() в языке С. Таким образом, просто записывая выражение "делимое / делитель", мы можем получить целую и дробную части одновременно.
Определение процесса деления

Частное - это результат деления числа на другое число без остатка. Остаток - это неразделимая часть исходного числа, та часть, которая не входит в частное.
Процесс деления состоит из нескольких шагов:
- Шаг 1: Записывается делимое (число, которое делится) и делитель (число, на которое делится).
- Шаг 2: Определяется кратчайшее количество раз, которое делитель умещается в делимом. Это число называется частным.
- Шаг 3: Полученное частное записывается сверху, а делитель записывается слева от него.
- Шаг 4: Вычитается произведение разности между делимым и частным и делителем. Это дает остаток.
- Шаг 5: Если остаток равен нулю, то деление завершается. Если остаток не равен нулю, то идет следующая итерация, в которой делимое становится равным остатку, а делитель остается прежним.
Таким образом, процесс деления позволяет находить части из целых чисел при делении и получать их частное и остаток. Этот метод широко используется в математике и других областях, где требуется разделение чисел на равные или близкие части.
Деление и его сущность

В математике деление обозначается символом "/". Например, 10/2 = 5, где 10 - делимое, 2 - делитель, а 5 - частное. Если при делении числа нацело, то остаток равен нулю.
Деление выполняется по определенным правилам, которые помогают найти частное и остаток. При делении целого числа на другое целое число можно получить следующие результаты:
| Делимое | Делитель | Частное | Остаток |
|---|---|---|---|
| 10 | 3 | 3 | 1 |
| 15 | 4 | 3 | 3 |
| 20 | 5 | 4 | 0 |
Частное при делении может быть как целым числом, так и десятичной дробью. Если делитель равен нулю, то деление невозможно и ошибка будет возникать.
Деление - это важная операция в математике, применяемая во многих областях, таких как физика, экономика, технические науки и другие. Знание основ деления и умение выполнять деление помогают в решении различных задач и расчетах.
Метод нахождения целой части от деления

Целая часть от деления может быть найдена с помощью простого алгоритма деления в столбик. Для выполнения этого алгоритма, следуйте следующим шагам:
- Разделите делимое на делитель.
- Запишите результат в виде десятичной дроби.
- Отсечь все десятичные цифры, оставив только целую часть.
- Это число будет являться целой частью от деления.
Например, рассмотрим следующий пример: 15 делить на 4. Применяя алгоритм деления в столбик, мы получим следующий результат:
| 15 | | | 4 | → | 3 |
Таким образом, целая часть от деления числа 15 на 4 равна 3.
Этот метод может быть использован для нахождения целой части от деления любых чисел. Всегда важно помнить, что результат будет целым числом без десятичных частей.
Метод деления в столбик с остатком
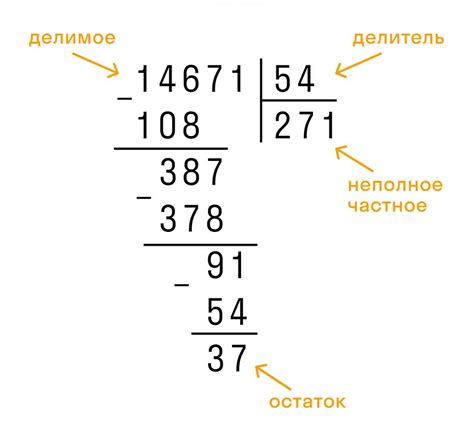
Для начала, необходимо записать делимое и делитель в столбик, причем делитель должен быть меньше делимого. Затем рассматриваются первые цифры делимого и делителя. Если делитель больше делимого, подходящий результат не может быть получен, и мы переходим к рассмотрению следующих цифр. Если делитель меньше делимого, мы проводим деление и записываем частное над делителем.
Далее, необходимо умножить записанное частное на делитель и вычесть полученное произведение из делимого. Остаток записывается под делимым числом. Затем мы переходим к следующей цифре делимого после записанного остатка и продолжаем деление.
Процесс повторяется до тех пор, пока не рассмотрены все цифры делимого. В конечном итоге, последовательность частичных результатов и остатков дает полное решение деления.
Метод деления в столбик с остатком может быть особенно полезным при делении больших чисел или в ситуациях, когда нужно получить дробный результат или точный остаток. Он также помогает в понимании процесса деления и способствует развитию навыков работы с числами.
Модульное деление и нахождение остатка
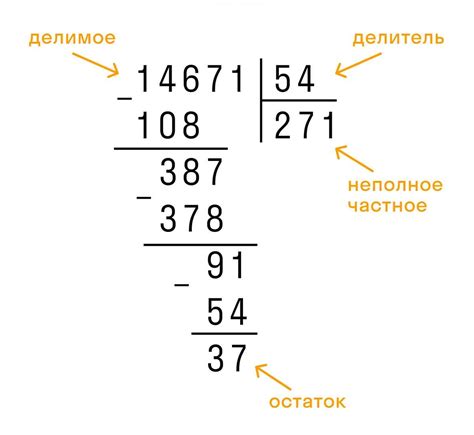
Пример:
| Деление | Остаток |
|---|---|
| 10 % 3 | 1 |
| 7 % 2 | 1 |
| 15 % 4 | 3 |
В таблице приведены различные примеры модульного деления. Первый столбец - это делимое число, второй столбец - это делитель, третий столбец - это остаток от деления.
Модульное деление часто используется для проверки четности или нечетности числа. Если остаток от деления на 2 равен 0, то число четное, иначе - нечетное.
Пример:
| Число | Остаток от деления на 2 | Четность |
|---|---|---|
| 10 | 0 | Четное |
| 7 | 1 | Нечетное |
| 15 | 1 | Нечетное |
В таблице приведены примеры проверки четности или нечетности чисел с помощью модульного деления.
Определение модульного деления

Для выполнения модульного деления мы используем знак процента (%). Формула для модульного деления выглядит следующим образом:
a % b = c
где a - делимое число, b - делитель, и c - остаток.
Например, при модульном делении числа 17 на 5, мы получим остаток 2, так как 17 % 5 = 2.
Важно отметить, что результат модульного деления всегда будет меньше делителя. Например, при модульном делении числа 10 на 3, мы получим остаток 1, так как 10 % 3 = 1.
Модульное деление имеет множество применений в программировании, так как позволяет удобно определять четность или нечетность числа, работать с круговыми вычислениями и многое другое.
Арифметический метод нахождения целой части

Арифметический метод представляет собой один из способов нахождения целой части при делении двух чисел. Этот метод основан на особенностях арифметики и позволяет получить точный результат без использования округления.
Для начала необходимо записать делимое и делитель. Затем, пошагово, нужно проследить, какие действия выполняются при делении, чтобы определить целую часть.
Шаг 1. Проверка знака.
Определяется знак полученного результата - он будет совпадать со знаком делимого.
Шаг 2. Расчет целой части.
Используя основные правила арифметики, выполняются действия предусмотренные делением. При делении число делимое делится на делитель, и результатом является целая часть.
Шаг 3. Определение остатка.
Для определения остатка при делении используется формула: остаток = делимое - (целая часть * делитель). Полученный остаток может быть положительным или отрицательным, в зависимости от знака делимого и делителя.
Арифметический метод является математически точным и позволяет получать результат без округления. Этот метод особенно полезен в задачах, где точность играет важную роль.
Алгоритм деления числа на цифру

Для выполнения данного алгоритма деления числа на цифру рекомендуется использовать следующие шаги:
- Начните с первой цифры числа, пройдите по всем цифрам числа, слева направо.
- Примените деление первой цифры на заданную цифру.
- Запишите результат деления первой цифры и остаток.
- Перенесите остаток в следующую итерацию и продолжайте деление по тому же алгоритму.
- Повторите шаги 2-4 для всех цифр числа.
Пример:
- Пусть у нас есть число 1234 и мы хотим разделить его на цифру 2.
- Применяем деление первой цифры 1 на цифру 2. Результат деления равен 0, остаток равен 1.
- Переносим остаток 1 в следующую итерацию.
- Применяем деление второй цифры 2 + остатка 1 = 21 на цифру 2. Результат деления равен 10, остаток равен 1.
- Переносим остаток 1 в следующую итерацию.
- Применяем деление третьей цифры 2 + остатка 1 = 21 на цифру 2. Результат деления равен 10, остаток равен 1.
- Переносим остаток 1 в следующую итерацию.
- Применяем деление четвертой цифры 2 + остатка 1 = 21 на цифру 2. Результат деления равен 10, остаток равен 1.
Таким образом, результатом деления числа 1234 на цифру 2 будет число 1010 с остатком 1.