Эйлеров цикл - это путь в графе, который проходит по каждому ребру ровно один раз и возвращается в исходную вершину. Такой цикл назван в честь известного швейцарского математика Леонарда Эйлера, который первым изучил данное свойство графов.
Найти эйлеров цикл в графе может быть непростой задачей, особенно в сложных сетях. Однако, существует несколько способов, которые помогают решить эту задачу. В данной статье рассмотрим некоторые из них.
Первый способ основан на использовании алгоритма Флёри. Он предполагает последовательное удаление ребер из графа, пока все они не будут использованы. Этот метод достаточно прост в реализации и позволяет найти эйлеров цикл в графе, если такой цикл существует.
Второй способ основан на использовании алгоритма Хирхолца. Он использует метод "разделяй и властвуй", разбивая граф на подграфы, отыскивая в каждом из них эйлеров цикл, а затем объединяя их в один общий цикл. Этот метод более эффективен, чем алгоритм Флёри, однако требует более сложной реализации.
Что такое эйлеров цикл в графе?

Эйлеров цикл существует только в связных графах, в которых каждая вершина имеет четную степень. Степень вершины определяется количеством ребер, выходящих из этой вершины. Если граф удовлетворяет этому условию, то можно найти эйлеров цикл.
Для поиска эйлерова цикла используются различные алгоритмы, такие как алгоритм Флёри или алгоритм Касарди. Они позволяют найти эйлеров цикл в графе за линейное время, то есть за время, пропорциональное количеству вершин и ребер.
Эйлеров цикл широко применяется в различных областях, таких как транспортное планирование, графический дизайн, сетевое планирование и другие. Он помогает оптимизировать пути и связи между различными объектами.
Эйлеров цикл имеет большое значение в теории графов и находит применение во множестве практических задач. Понимание этого понятия помогает решать различные задачи, связанные с поиском оптимальных путей и маршрутов.
Перебор всех возможных путей
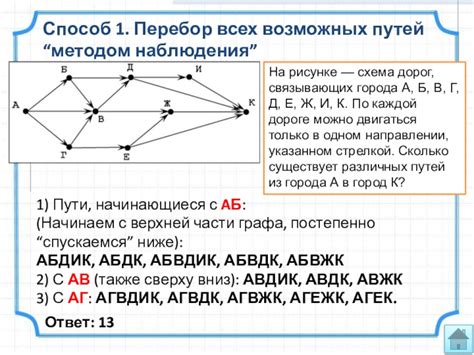
Для применения этого метода необходимо составить список всех возможных путей, каждый из которых начинается с одной из вершин графа и проходит через все ребра. Затем производится перебор всех возможных комбинаций этих путей, чтобы найти циклы, удовлетворяющие условиям эйлерова цикла.
Однако следует отметить, что этот метод имеет высокую вычислительную сложность, особенно для больших графов. В худшем случае, при отсутствии эйлерова цикла, необходимо перебрать все возможные комбинации путей, что может занять большое количество времени.
Кроме того, для применения этого метода необходимо иметь полную информацию о графе, включая все его ребра и вершины. В противном случае, перебор всех возможных путей может быть неполным или некорректным.
В целом, метод перебора всех возможных путей является одним из способов поиска эйлерова цикла в графе, но его эффективность может быть снижена из-за высокой вычислительной сложности и необходимости полной информации о графе.
Метод Флёри
Алгоритм метода Флёри:
- Выбираем произвольную вершину графа в качестве текущей вершины.
- Если у текущей вершины есть непосещенные ребра, перемещаемся по одному из них в соседнюю вершину и удаляем это ребро.
- Если у текущей вершины нет непосещенных ребер, добавляем текущую вершину в результат. Возвращаемся к предыдущей вершине и продолжаем поиск.
- Повторяем шаги 2-3 до тех пор, пока не будут посещены все ребра графа.
Если после выполнения алгоритма все ребра будут удалены и граф станет несвязным, то в нем нет эйлерова цикла. В противном случае, полученный путь будет являться эйлеровым циклом.
Алгоритм Хирнока и Мурая
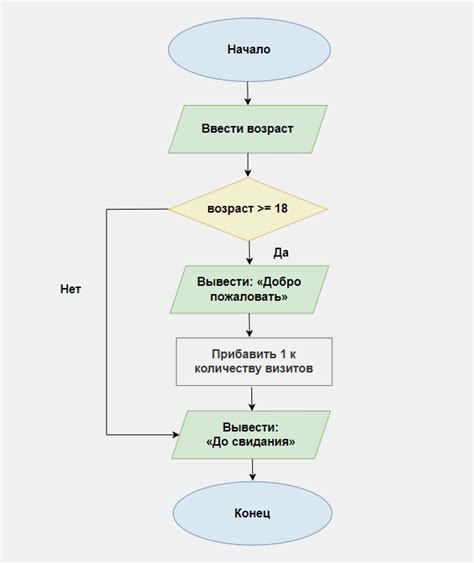
1. Проверка наличия эйлерова цикла: сначала проверяем, является ли граф связным и имеет все вершины четной степени. Если эти условия не выполняются, то в графе отсутствует эйлеров цикл.
2. Построение стека (H): в стек H помещается вершина, из которой также вставляется в новый граф. Пока стек не пуст, из него удаляется вершина, и все ее соседние вершины добавляются в H в случае, если ребро, соединяющее текущую вершину и соседнюю, не является мостом.
3. Процедура удаления мостов: в новый граф постепенно добавляются ребра, и для каждого нового ребра проверяется, не стал ли он мостом. Если после добавления ребра граф становится несвязным, оно удаляется.
5. Финальные шаги: после нахождения эйлерова цикла, можно вывести его в нужном формате (например, последовательность вершин).
Алгоритм Хирнока и Мурая довольно эффективен и позволяет найти эйлеров цикл в графе за линейное время.
Поиск в глубину

Алгоритм поиска Эйлерова цикла в графе с использованием поиска в глубину выполняет следующие шаги:
- Выбор стартовой вершины. Выбирается любая вершина графа в качестве стартовой.
- Пометка посещенных ребер. Все ребра графа помечаются как непосещенные.
- Рекурсивный поиск в глубину. Начиная с выбранной стартовой вершины, происходит глубинный обход графа вплоть до тех пор, пока не будут посещены все вершины и ребра.
- Проверка наличия Эйлерова цикла. После завершения обхода проверяется количество посещенных ребер. Если количество посещенных ребер равно общему количеству ребер в графе, то Эйлеров цикл существует.
- Формирование Эйлерова цикла. При наличии Эйлерова цикла, происходит формирование последовательности вершин графа, образующих цикл.
Описанный алгоритм обеспечивает эффективный способ поиска Эйлерова цикла в графе с использованием поиска в глубину.
Метод Фриша и Райтмайстера

Алгоритм состоит из следующих шагов:
- Выбирается произвольная вершина графа, которая будет являться начальной вершиной для построения эйлерова цикла.
- На каждом шаге алгоритма выбирается такое ребро, которое не входит в построенный эйлеров цикл, но при его добавлении образуется цикл.
- При обнаружении такого ребра, алгоритм производит его добавление в цикл и переход к следующей вершине.
- Если все ребра уже пройдены, но образовать эйлеров цикл не удалось, алгоритм производит обратный ход и удаляет последнее добавленное ребро.
- Алгоритм продолжает работу до тех пор, пока не будет построен эйлеров цикл, либо не будут пройдены все возможные ребра графа.
Метод Фриша и Райтмайстера является эффективным способом поиска эйлерова цикла и может применяться на практике для решения задач, связанных с обходом графов.