Пирамиды - одно из самых интересных и загадочных геометрических тел. Они привлекают внимание своей необычной формой и могут быть использованы в различных областях науки и практики. Однако, чтобы изучать свойства пирамиды, необходимо знать ее величины, в том числе и ее объем. В данной статье мы рассмотрим, как найти объем пирамиды по координатам вершин.
Для начала, нужно запомнить, что пирамида - это геометрическое тело, у которого есть одна вершина и плоская фигура, называемая основанием. Основание может быть любой плоской фигурой: квадрат, прямоугольник, треугольник и т.д. Координаты вершин пирамиды определяют ее форму и положение в пространстве.
Чтобы найти объем пирамиды по ее вершинам, необходимо знать площадь основания и высоту пирамиды. Площадь основания можно найти с помощью формулы для площади плоской фигуры, а высоту пирамиды можно найти с помощью теоремы Пифагора или трехмерной теоремы косинусов.
Как определить объем пирамиды по координатам вершин
Первым шагом необходимо найти площадь основания пирамиды. Для этого можно использовать формулу площади треугольника, если основание пирамиды представлено треугольником. Если основание является многоугольником, то следует разбить его на треугольники и найти сумму площадей. Для нахождения площади треугольника можно использовать формулу Герона или формулу половины произведения сторон на синус угла между ними.
Затем необходимо найти высоту пирамиды. Для этого можно использовать формулу, которая основана на нахождении расстояния между основанием и вершиной пирамиды. Если пирамида задана в пространстве, то расстояние можно найти с использованием формулы для нахождения расстояния между двумя точками в трехмерном пространстве.
И наконец, можно найти объем пирамиды, используя формулу: V = (S * h) / 3, где V - объем пирамиды, S - площадь основания, h - высота пирамиды. Полученный результат будет выражен в единицах измерения площади умноженных на единицы измерения длины.
Пример:
| Координаты вершин | Длины сторон |
|---|---|
| A(0, 0, 0) | a = 5 |
| B(5, 0, 0) | b = 6 |
| C(2, 3, 0) | c = 4 |
| D(2.5, 1.5, 4) |
Для пирамиды с координатами вершин A(0, 0, 0), B(5, 0, 0), C(2, 3, 0) и D(2.5, 1.5, 4) нужно сначала найти площадь основания:
S = SABC = SABD + SBCD + SCAD
Площадь треугольника ABC можно найти с помощью формулы Герона:
SABC = √(p * (p - a) * (p - b) * (p - c)), где p - полупериметр треугольника ABC
Полупериметр треугольника ABC равен:
p = (a + b + c) / 2
Подставляя значения сторон треугольника ABC в формулу, получим:
p = (5 + 6 + 4) / 2 = 7.5
SABC = √(7.5 * (7.5 - 5) * (7.5 - 6) * (7.5 - 4)) ≈ 9.9216
Аналогично можно найти площади треугольников ABD и BCD:
SABD = √(p1 * (p1 - a) * (p1 - b) * (p1 - d))
где p1 - полупериметр треугольника ABD
p1 = (a + b + d) / 2 = (5 + 6 + 4) / 2 = 7.5
SABD = √(7.5 * (7.5 - 5) * (7.5 - 6) * (7.5 - 4)) ≈ 9.9216
SBCD = √(p2 * (p2 - b) * (p2 - c) * (p2 - d))
где p2 - полупериметр треугольника BCD
p2 = (b + c + d) / 2 = (6 + 4 + 4) / 2 = 7
SBCD = √(7 * (7 - 6) * (7 - 4) * (7 - 4)) ≈ 6.9282
SCAD = √(p3 * (p3 - a) * (p3 - c) * (p3 - d))
где p3 - полупериметр треугольника CAD
p3 = (a + c + d) / 2 = (5 + 4 + 4) / 2 = 6.5
SCAD = √(6.5 * (6.5 - 5) * (6.5 - 4) * (6.5 - 4)) ≈ 5.4373
Теперь находим площадь основания:
S = SABC + SABD + SBCD + SCAD ≈ 9.9216 + 9.9216 + 6.9282 + 5.4373 ≈ 32.2087
Затем находим высоту пирамиды:
h = AD = √((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2)
где (x1, y1, z1) и (x2, y2, z2) - координаты вершин D и A пирамиды
h = √((2.5 - 0)2 + (1.5 - 0)2 + (4 - 0)2) = √(6.25 + 2.25 + 16) = √24.5 ≈ 4.9497
Наконец, найдем объем пирамиды:
V = (S * h) / 3 = (32.2087 * 4.9497) / 3 ≈ 52.7058
Таким образом, объем пирамиды, заданной координатами вершин A(0, 0, 0), B(5, 0, 0), C(2, 3, 0) и D(2.5, 1.5, 4), составляет около 52.7058 единицы объема.
Определение пирамиды
У пирамиды есть несколько характеристик:
- Основание - это многоугольник, на котором стоит пирамида.
- Высота пирамиды - это расстояние между вершиной и плоскостью основания.
- Грани - это поверхности, образованные боковыми сторонами пирамиды.
- Ребра - это отрезки, соединяющие вершину пирамиды с вершинами основания.
- Вершина - это точка, в которой сходятся все грани пирамиды.
- Объём пирамиды - это количество пространства, занимаемое пирамидой. Он может быть определен различными способами, включая формулу, основанную на координатах вершин пирамиды.
Определение пирамиды поможет нам лучше понять ее структуру и основные характеристики, что в дальнейшем позволит нам рассчитать ее объем и решить множество задач в геометрии.
Координаты вершин пирамиды

Для нахождения объема пирамиды по координатам вершин необходимо знать координаты каждой из вершин пирамиды. Координаты вершин можно представить в виде таблицы, где каждая строка соответствует одной вершине и содержит значения координат x, y и z.
Пример таблицы с координатами вершин пирамиды:
| Вершина | x | y | z |
|---|---|---|---|
| Вершина A | xA | yA | zA |
| Вершина B | xB | yB | zB |
| Вершина C | xC | yC | zC |
| Вершина D | xD | yD | zD |
Где x, y и z - координаты вершин пирамиды, а A, B, C и D - обозначения вершин.
Зная координаты вершин, можно приступить к вычислению объема пирамиды по формуле. Необходимые шаги и значения можно найти в соответствующей статье.
Нахождение основания пирамиды
Для нахождения основания пирамиды по координатам вершин необходимо рассмотреть плоскость, на которой лежит пирамида. Основание пирамиды представляет собой многоугольник, образованный пересечением этой плоскости с боковыми гранями пирамиды.
Координаты вершин пирамиды могут быть заданы в трехмерном пространстве, например, в виде троек чисел (x, y, z). Для нахождения основания пирамиды производится проекция вершин на плоскость, то есть отбрасываются координаты z, оставляя только координаты x и y.
После проекции вершин на плоскость можно получить множество точек, образующих основание пирамиды. Для этого можно использовать алгоритмы построения многоугольников, такие как алгоритм Джарвиса или алгоритм Грэхема.
Алгоритм Джарвиса (или алгоритм оболочки) начинается с выбора самой левой (или самой правой) из всех вершин пирамиды. Затем выбранная вершина рассматривается как текущая, и на каждом шаге алгоритма находится следующая вершина, образующая наименьший угол с текущей вершиной. Процесс повторяется до тех пор, пока следующая вершина не будет совпадать с первой. Все выбранные вершины образуют периметр многоугольника - это и будет основание пирамиды.
Алгоритм Грэхема состоит в следующем: выбирается самая нижняя и самая левая вершина пирамиды. Затем все остальные вершины сортируются по углу, образуемому соединительной линией между текущей вершиной и выбранным исходным основанием пирамиды. После сортировки выбирается первая вершина и производится обход всех вершин, при этом каждая новая вершина добавляется в основание пирамиды только в случае, если она не образует правый поворот относительно двух последних вершин из основания.
После выполнения алгоритма Джарвиса или алгоритма Грэхема, основание пирамиды будет представлять собой множество вершин, образующих многоугольник. Из такого множества точек можно вычислить площадь основания пирамиды и применить соответствующую формулу для нахождения ее объема.
Вычисление высоты пирамиды
Высота пирамиды может быть вычислена, исходя из координат вершин. Для этого можно воспользоваться формулой:
Высота = расстояние от вершины до плоскости основания / проекция плоскости основания на плоскость, параллельную координатной оси.
Для вычисления расстояния от вершины до плоскости основания можно воспользоваться формулой длины вектора:
Расстояние = √((x - x₁)² + (y - y₁)² + (z - z₁)²), где (x₁, y₁, z₁) - координаты вершины, а (x, y, z) - координаты точки на плоскости основания.
А проекцию плоскости основания можно вычислить, если заменить координаты вершины и координаты точки на плоскости основания на соответствующие координаты их проекций.
Найдя эти два значения, можно подставить их в формулу высоты пирамиды и получить искомое значение высоты.
Определение площади основания пирамиды
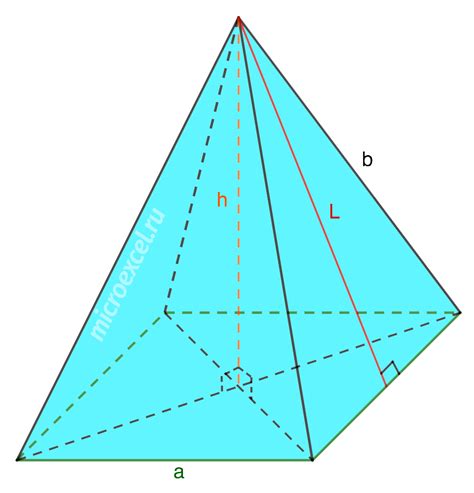
Если пирамида имеет правильную геометрическую форму, то площадь основания можно вычислить по известной формуле. Например, для пирамиды с квадратным основанием площадь вычисляется как квадрат стороны основания:
S = a^2
Где S - площадь основания, а a - длина стороны квадрата.
Если же пирамида имеет неправильную форму, то площадь основания можно вычислить с помощью различных методов геометрии и математики.
Важно отметить, что для каждого типа пирамиды будет своя формула расчета площади основания. Поэтому перед началом вычислений необходимо точно определить геометрические параметры пирамиды.
Имея точные координаты вершин пирамиды, можно приступать к определению ее площади основания и затем рассчитывать ее объем с использованием соответствующих формул и методов.
Формула для вычисления объема пирамиды

Объем пирамиды может быть вычислен по формуле:
- Найдите длину основания пирамиды, используя координаты вершин. Для этого примените формулу расстояния между двумя точками в трехмерном пространстве.
- Определите высоту пирамиды. Это расстояние от вершины пирамиды до плоскости, на которой лежит основание.
- Умножьте площадь основания на высоту и разделите на 3, чтобы получить объем пирамиды.
В общем виде формула для вычисления объема пирамиды выглядит следующим образом:
Объем = (Площадь основания * Высота) / 3
Где:
- Объем - объем пирамиды
- Площадь основания - площадь основания пирамиды
- Высота - высота пирамиды
Используя данную формулу, можно легко вычислить объем пирамиды, зная координаты ее вершин.
Практический пример

Давайте рассмотрим практический пример использования формулы для нахождения объема пирамиды по координатам ее вершин.
Предположим, у нас есть пирамида с вершинами A(1, 2, 3), B(4, 5, 6), C(7, 8, 9) и D(10, 11, 12). Наша задача - найти объем этой пирамиды.
По известной формуле, объем пирамиды можно найти как треть произведения площади основания на высоту пирамиды.
Сначала найдем площадь основания пирамиды ABCD. Для этого построим векторы AB и AC.
AB = (4 - 1, 5 - 2, 6 - 3) = (3, 3, 3)
AC = (7 - 1, 8 - 2, 9 - 3) = (6, 6, 6)
Теперь найдем векторное произведение векторов AB и AC.
AB x AC = ((3 * 6 - 3 * 6), (3 * 6 - 3 * 6), (3 * 6 - 3 * 6)) = (0, 0, 0)
Площадь основания пирамиды ABCD равна половине модуля векторного произведения AB x AC:
S = 1/2 * sqrt(0^2 + 0^2 + 0^2) = 0
Теперь найдем высоту пирамиды. Для этого построим вектор AD.
AD = (10 - 1, 11 - 2, 12 - 3) = (9, 9, 9)
Высота пирамиды равна длине вектора AD:
h = sqrt(9^2 + 9^2 + 9^2) = 9 * sqrt(3)
Итак, объем пирамиды ABCD равен одной трети произведения площади основания на высоту:
V = 1/3 * S * h = 1/3 * 0 * 9 * sqrt(3) = 0
Таким образом, пирамида с вершинами A(1, 2, 3), B(4, 5, 6), C(7, 8, 9) и D(10, 11, 12) имеет объем, равный 0.
Важные моменты при нахождении объема пирамиды
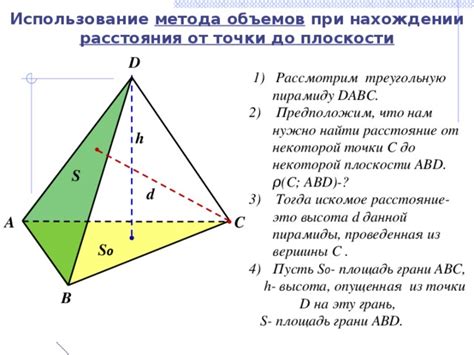
При нахождении объема пирамиды по координатам вершин необходимо учесть ряд важных моментов:
- Вершины пирамиды должны быть заданы в трехмерном пространстве с помощью координат x, y и z.
- Пирамида должна быть правильной, то есть иметь основание, которое является многоугольником и все боковые грани пирамиды должны быть треугольниками.
- Необходимо проверить, что вершины, образующие основание пирамиды, расположены в одной плоскости.
- Дополнительно необходимо проверить, что основание пирамиды не самопересекается.
Учтя эти важные моменты, можно приступить к использованию формулы для нахождения объема пирамиды по ее вершинам:
V = 1/6 * [x1(y2z3 - y3z2) + x2(y3z1 - y1z3) + x3(y1z2 - y2z1)]
Где x1, y1 и z1 - координаты первой вершины пирамиды, x2, y2 и z2 - координаты второй вершины, а x3, y3 и z3 - координаты третьей вершины.