Синус - одна из основных тригонометрических функций, которая широко применяется в различных областях науки и инженерии. Нахождение синуса в треугольниках без прямого угла является важной задачей, которая имеет множество практических применений, включая геодезию, физику, компьютерную графику и другие области.
Существует несколько эффективных методов расчета синуса в треугольниках без прямого угла. Один из них - использование формулы полупериметра и площади треугольника в сочетании с теоремой синусов. По этим данным можно определить длины сторон треугольника и затем вычислить синус заданного угла. Этот метод позволяет получить точный результат, но требует выполнения нескольких шагов расчета.
Другой метод заключается в использовании геометрической интерпретации синуса треугольника. В данном случае, можно воспользоваться радиусом описанной окружности треугольника и длинами его сторон для вычисления требуемого синуса. Этот метод обеспечивает более простой способ расчета синуса в треугольнике без прямого угла и может быть применен в различных ситуациях.
В данной статье мы рассмотрим эти и другие эффективные методы нахождения синуса в треугольниках без прямого угла подробнее. Разберем применение формул и вычислительные алгоритмы для получения точных результатов. Помимо этого, мы также рассмотрим примеры задач, в которых нахождение синуса в треугольниках без прямого угла является необходимой задачей. Эта информация будет полезной для студентов, ученых и специалистов в различных областях, где требуется работа с треугольниками и тригонометрическими функциями.
Способы нахождения синуса
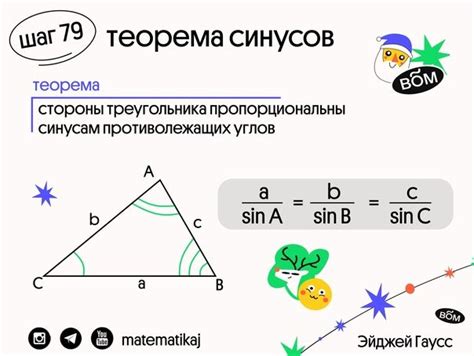
Первый способ - использование формулы синусов. Если известны длины двух сторон треугольника и величина между ними угла, то синус этого угла можно вычислить по следующей формуле:
| Формула | Описание |
|---|---|
| sin(A) = a / c | где A - между двумя известными сторонами a и c |
| sin(B) = b / c | где B - между двумя известными сторонами b и c |
| sin(C) = a / b | где C - между двумя известными сторонами a и b |
Второй способ - использование правил синусов. Если известны длины двух сторон треугольника и величина противолежащего угла, то синус этого угла можно вычислить по следующей формуле:
| Формула | Описание |
|---|---|
| sin(A) = a / b | где A - угол, противолежащий стороне a |
| sin(B) = b / a | где B - угол, противолежащий стороне b |
| sin(C) = c / a | где C - угол, противолежащий стороне c |
Оба этих способа позволяют находить синус треугольника без прямого угла и являются частными случаями общей формулы для нахождения синуса в произвольном треугольнике. Умение использовать эти способы является важным навыком в решении задач, связанных с треугольниками.
Сегментирование треугольников
Для эффективного нахождения синуса в треугольниках без прямого угла можно использовать метод сегментирования треугольников. Этот метод позволяет разбить исходный треугольник на несколько более маленьких треугольников, в которых будет проще производить вычисления.
Принцип метода заключается в разделении треугольника на подтреугольники, в каждом из которых будет прямой угол. Затем, используя формулы нахождения синуса в прямоугольном треугольнике, можно рассчитать синусы каждого из подтреугольников. Затем, используя формулы вычисления синусов при сумме и разности углов, можно получить значение синуса исходного треугольника.
Применение метода сегментирования треугольников позволяет значительно упростить вычисления и снизить вероятность ошибок. Также этот метод может быть использован для других расчетов, связанных с треугольниками, например, нахождения косинуса или тангенса.
Формула полусуммы косинусов
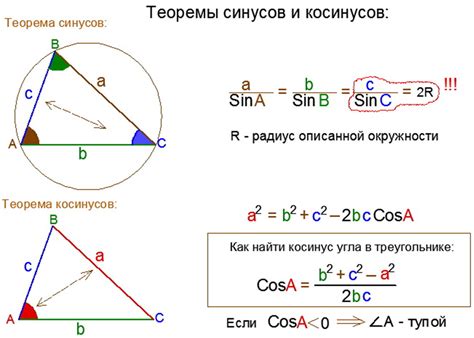
Формула выглядит следующим образом:
sin(A + B) = 2sin((A + B)/2)cos((A - B)/2)
Где A и B - углы треугольника.
Для того чтобы найти синус одного из углов, необходимо знать значения других двух углов и применить формулу полусуммы косинусов, заменив в ней углы на известные значения.
Этот метод очень удобен при решении задач на нахождение синуса в треугольнике без прямого угла, так как позволяет вычислить значение синуса по известным углам без использования таблиц или калькуляторов.
Разделение треугольников на два прямоугольных
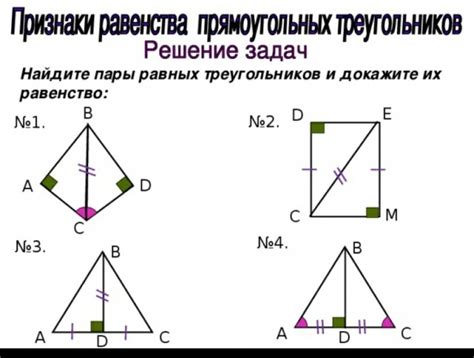
Для применения данного метода необходимо найти на треугольнике сторону, противолежащую искомому углу, и разделить треугольник на два прямоугольных под требуемым углом. Затем, применяя формулу синуса, можно найти значение синуса искомого угла.
Процесс разделения треугольника на два прямоугольных может быть проиллюстрирован следующим образом:
- Найдите сторону, противолежащую искомому углу.
- Нарисуйте линию, перпендикулярную данной стороне, и проходящую через вершину искомого угла.
- Полученная линия разделит треугольник на два прямоугольных под требуемым углом.
Используя полученные прямоугольники, можно применить формулу синуса для расчета значения синуса искомого угла. Таким образом, можно эффективно находить значения синуса в треугольниках без прямого угла.
Метод суммы площадей треугольников

Для применения этого метода необходимо знать длины двух сторон треугольника и величину угла, образованного этими сторонами. Для иллюстрации рассмотрим следующую ситуацию:
Пусть треугольник ABC имеет стороны a и b, а угол между ними равен γ. Чтобы найти синус этого угла, можно воспользоваться следующей формулой:
sin(γ) = 2S / (a * b)
где S – площадь треугольника ABC.
Для нахождения площади треугольника ABC можно воспользоваться формулой Герона:
S = sqrt(p * (p - a) * (p - b) * (p - c))
где p – полупериметр треугольника ABC, который вычисляется по формуле:
p = (a + b + c) / 2
Зная длины сторон треугольника и значение угла γ, можно с легкостью вычислить синус угла γ при помощи метода суммы площадей треугольников. Этот метод позволяет проводить точные и быстрые расчеты синуса в треугольниках без прямого угла.
Степени треугольников
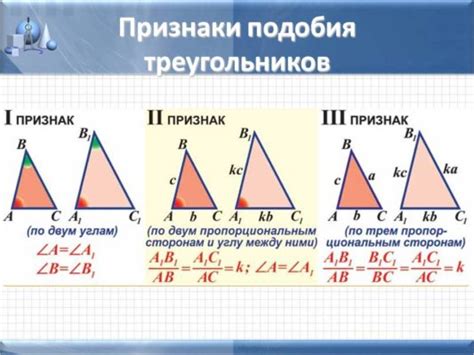
Для треугольников без прямого угла степень может принимать значения в диапазоне от 0 до 180 градусов. Если сумма углов треугольника равна 180 градусов, то его степень равна 0.
Если степень треугольника больше 0, то он называется остроугольным. Это означает, что все его углы меньше 90 градусов. Чем ближе степень к 180 градусам, тем более остроугольным является треугольник.
Если степень треугольника равна 90 градусам, то он называется прямоугольным. В таком треугольнике один из его углов является прямым углом.
Если степень треугольника больше 90 градусов, то он называется тупоугольным. Это означает, что у одного из его углов больше 90 градусов.
Знание степеней треугольников позволяет лучше понять и анализировать их свойства и характеристики. Также степени треугольников полезны при решении различных задач и задачек.
Угол и пропорция
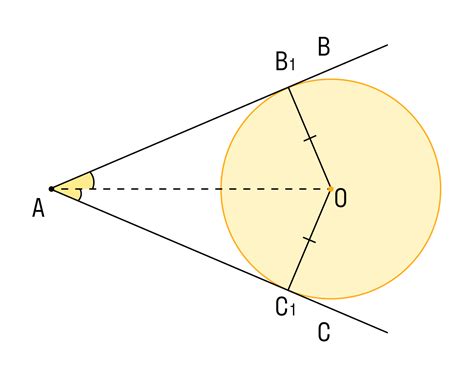
В геометрии существует связь между углами и пропорциями сторон в треугольниках без прямого угла. Это позволяет найти синус угла, используя известные значения сторон.
Для начала, рассмотрим треугольник ABC, где угол A равен α. Пусть сторона AB имеет длину a, сторона BC имеет длину b, и сторона AC имеет длину c. Мы хотим найти синус угла α.
Используя теорему синусов, мы можем записать следующее соотношение:
| sin α | = | a / c |
Теперь, если мы знаем значения сторон a и c, мы можем выразить синус угла α в виде пропорции. Если мы хотим найти длину стороны c, мы можем переставить значения и получить следующее соотношение:
| c | = | a / sin α |
Это позволяет нам выразить синус угла α в зависимости от известных значений сторон треугольника. Таким образом, мы можем использовать пропорции и тригонометрические соотношения для эффективного нахождения синуса в треугольниках без прямого угла.
Использование смежности углов
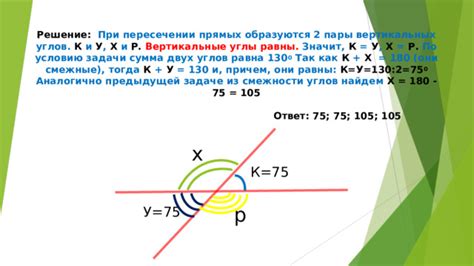
Для применения этого метода нужно знать значения двух смежных углов и соответствующие им стороны треугольника. Сначала необходимо найти индекс синуса одного из смежных углов (например, A). Для этого используется соотношение sin A = sin (180 - A). Затем можно использовать соответствующие пропорции для нахождения значения синуса нужного угла. Например, если известно sin A и сторона a, нужно найти sin B, то можно воспользоваться пропорцией sin A/a = sin B/b, где b - смежная сторона треугольника.
Использование смежности углов позволяет эффективно рассчитывать значения синуса в треугольниках без прямого угла и использовать их для решения различных задач в геометрии, физике и других науках.
