Конус – это геометрическое тело, которое имеет форму треугольника, у которого одна из сторон является основанием, а остальные две стороны соединены в одной точке, называемой вершиной. Образующая конуса – это линия, соединяющая вершину конуса со всеми точками его основания. Для вычисления различных параметров конуса, включая его высоту, можно использовать различные формулы и методы, в зависимости от имеющихся данных.
Если известны образующая и радиус основания конуса, то высоту можно вычислить при помощи теоремы Пифагора. Для этого необходимо вначале найти длину радиуса основания, используя формулу R = d/2, где d – диаметр основания. Затем, подставив значения образующей и радиуса в формулу катета и гипотенузы прямоугольного треугольника, можно найти высоту конуса, применяя формулу h = √(l^2 - R^2), где h – высота, l – образующая, R – радиус основания.
Если же известны только образующая и угол между образующей и плоскостью основания конуса, то высоту можно найти с помощью тригонометрических функций. Можно воспользоваться формулой h = l * sin(α), где h – высота конуса, l – образующая, α – угол между образующей и плоскостью основания (в радианах).
Вычисление высоты конуса через образующую

Для вычисления высоты конуса через образующую необходимо знать длину образующей и радиус основания конуса.
Высота конуса можно найти с помощью теоремы Пифагора:
- Найдите квадрат радиуса основания конуса.
- Найдите квадрат длины образующей конуса.
- Вычислите разность между квадратом длины образующей и квадратом радиуса.
- Извлеките квадратный корень из полученного числа.
Полученное значение будет являться высотой конуса.
Пример:
- Пусть радиус основания конуса равен 4 см.
- Пусть длина образующей конуса равна 5 см.
- Вычислим квадрат радиуса: 4^2 = 16.
- Вычислим квадрат длины образующей: 5^2 = 25.
- Вычислим разность между квадратом длины образующей и квадратом радиуса: 25 - 16 = 9.
- Извлечем квадратный корень из полученного числа: √9 = 3.
Таким образом, высота конуса через образующую равна 3 см.
Определение высоты конуса
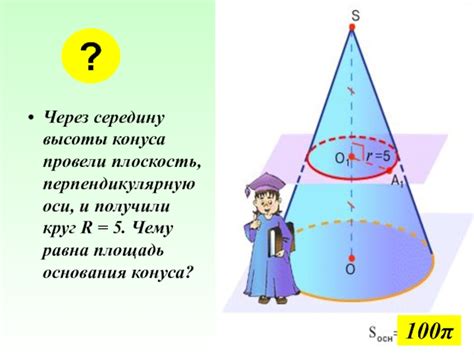
Чтобы определить высоту конуса, можно использовать теорему Пифагора или подобные треугольники:
- Если известны образующая (l) и радиус основания (r), то можно использовать теорему Пифагора для нахождения высоты (h) по формуле: h = √(l^2 - r^2)
- Если известны образующая (l) и высота (h), можно найти радиус основания (r) с помощью подобных треугольников: r = (h/l) * R, где R - радиус вершины конуса
Формула вычисления высоты конуса
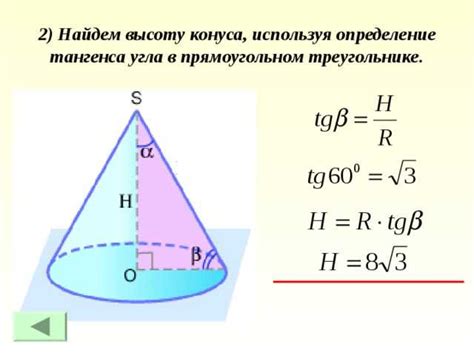
Для вычисления высоты конуса можно использовать следующую формулу:
h = √(r2 + l2),
где:
- h - высота конуса;
- r - радиус основания конуса;
- l - образующая конуса.
Данная формула основана на применении теоремы Пифагора для прямоугольного треугольника, образующегося между образующей и радиусом основания конуса.
Используя эту формулу, вы можете рассчитать высоту конуса, зная значения радиуса основания и образующей.
Пример решения

Для нахождения высоты конуса через образующую необходимо знать значение образующей и радиус основания конуса.
| Шаг | Действие | Результат |
| 1 | Найдите площадь основания конуса с помощью формулы: π * r^2, где π - приближенное значение числа Пи, r - радиус основания конуса. | Площадь основания конуса: S |
| 2 | Используйте формулу: V = (1/3) * S * h, где V - объем конуса, S - площадь основания конуса, h - высота конуса. | Подставьте значения из предыдущего шага и объема конуса: V, и найдите высоту конуса h. |
Таким образом, вы сможете найти высоту конуса через образующую и радиус основания.