Поиск части дроби - это базовое представление, которое школьники получают во время обучения математике в начальной школе. Оно позволяет разобраться в числовых понятиях и правилах работы с дробями. Знание этих способов помогает ученикам разбираться в задачах на смешанные числа, упрощать дроби и решать другие задачи, связанные с дробными числами.
Способы поиска части дроби имеют практическое значение для учащихся начальных классов, так как они помогают учиться делению с остатком, находить проценты и решать задачи по экономике. Знание этих способов также помогает школьникам развивать логическое мышление и аналитические навыки, необходимые для успешной учебы в дальнейшем.
Существует несколько основных способов поиска части дроби: разложение на сумму десятков и единиц, нахождение необходимого числа после запятой, вычисление процентного значение и другие. Каждый из этих способов имеет свои преимущества и может быть использован в разных ситуациях. Поэтому, начиная изучать дроби в 5 классе, ученики должны освоить основные способы поиска части дроби и научиться применять их в практике.
Как найти часть дроби в 5 классе

Способы поиска части дроби включают:
- Определение части целого числа: ученик должен определить, сколько частей целого числа нужно выбрать. Например, если у нас есть дробь 3/4 и нам нужно найти 3/4 часть целого числа 12, мы можем использовать умножение:
- Определение части объекта: в качестве предмета может быть обычный объект, например, яблоко. Ученик должен определить, сколько частей объекта нужно взять. Применяется тот же принцип умножения, что и в случае с целыми числами:
- Сравнение дробей: ученик должен сравнить две дроби и определить, какая из них больше или меньше. Если нам нужно выбрать часть числа или предмета, которая больше или меньше другой указанной части, мы можем воспользоваться этим методом:
3/4 * 12 = 9
3/4 * яблоко = 3/4 яблока
3/4 > 1/2
В 5 классе ученики узнают о различных способах нахождения части дроби и применяют их на практике. Это важные навыки, которые школьники могут использовать в реальной жизни для работы с дробями и различными количественными значениями.
Понятие дроби и ее составляющие
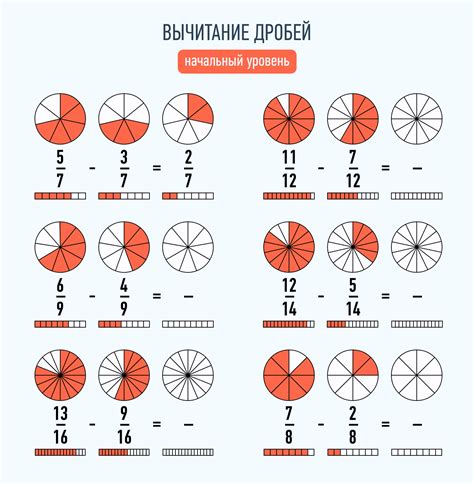
Числитель - это верхняя часть дроби, которая показывает количество выбранных частей.
Знаменатель - это нижняя часть дроби, которая показывает общее количество равных частей, из которых состоит целое.
Например, в дроби 3/4, числитель равен 3, что означает, что мы выбрали 3 из 4 равных частей целого.
Дроби могут быть представлены в различных форматах, таких как обыкновенные, десятичные и процентные дроби. Важно понимать, как работать с дробями и находить их части для решения математических задач.
Способы нахождения числителя

1. Использование дробной линейки. Дробная линейка представляет собой длинную прямую, разделенную на равные части. При использовании дробной линейки мы можем найти числитель дроби, определив, на каком отрезке расположена данная дробь. Например, для дроби 1/4 мы найдем отметку между 0 и 1 на дробной линейке.
2. Разделение числа на дробь. Другим способом нахождения числителя является разделение числа на дробь. Например, если у нас есть число 5 и дробь 1/4, мы можем разделить число на равные части, чтобы определить числитель. В данном случае, числитель будет равен 1, так как мы делим число на четыре равные части и берем первую часть.
3. Использование дробного деления. Один из наиболее распространенных способов нахождения числителя – это использование дробного деления. Для этого мы делим числитель на знаменатель и получаем результат. Например, для дроби 3/5 мы делим 3 на 5 и получаем числитель равный 0.6.
4. Применение таблицы умножения. Также можно использовать таблицу умножения для нахождения числителя. Если мы знаем, что 3/4 равно 0.75, мы можем найти числитель путем умножения 0.75 на 4. В данном случае, числитель будет равен 3.
Выбор способа нахождения числителя зависит от задачи и предпочтений ученика. Важно понять каждый способ и уметь применять его в разных ситуациях.
Способы нахождения знаменателя

В математике существуют различные способы нахождения знаменателя дроби. Рассмотрим некоторые из них:
- По определению: знаменатель - это число под чертой в дроби. Для нахождения знаменателя нужно посмотреть на число, которое стоит под чертой.
- Путем разложения: если дробь дана в виде суммы или разности двух чисел, можно узнать значение знаменателя, разложив каждое из чисел на множители и сократив полученные выражения.
- С помощью компонентов: если дробь дана в виде произведения двух чисел, знаменателем будет являться одно из этих чисел.
Это лишь несколько способов нахождения знаменателя. Вы можете выбрать тот метод, который вам наиболее удобен для решения конкретной задачи.
Примеры решения задач по поиску части дроби

Ниже приведены несколько примеров решения задач по поиску части дроби.
| Задача | Решение | Ответ |
|---|---|---|
| Найдите третью часть от дроби 4/5. | Для нахождения третьей части от дроби, мы должны разделить числитель на третье число (3): 4 ÷ 3 = 1.3333... Поэтому третья часть от дроби 4/5 равна 1.3333... | 1.3333... |
| Найдите половину от дроби 7/8. | Для нахождения половины от дроби, мы должны разделить числитель на второе число (2): 7 ÷ 2 = 3.5. Поэтому половина от дроби 7/8 равна 3.5. | 3.5 |
| Найдите четверть от дроби 2/3. | Для нахождения четверти от дроби, мы должны разделить числитель на четвертое число (4): 2 ÷ 4 = 0.5. Поэтому четверть от дроби 2/3 равна 0.5. | 0.5 |
Надеюсь, эти примеры помогут вам лучше понять, как находить часть дроби.