Геометрическая прогрессия – одна из самых важных математических концепций. Она была известна еще античным математикам, но ее свойства и приложения до сих пор активно изучаются и исследуются. В геометрической прогрессии каждый следующий элемент получается умножением предыдущего на определенное число, называемое знаменателем. Сумма первых n чисел геометрической прогрессии является одним из важнейших понятий, и для ее вычисления существуют различные методы и формулы.
Сумма первых n чисел геометрической прогрессии играет важную роль во многих областях науки, включая физику, экономику и информатику. Она позволяет решать широкий спектр задач, таких как вычисление суммы процентов по вкладу на определенный срок, оценка популяции организмов, изменение температуры тела в течение определенного времени и многое другое.
Существует несколько методов и формул для вычисления суммы первых n чисел геометрической прогрессии. Один из наиболее распространенных методов – использование общего закона геометрической прогрессии и алгебраического выражения для суммы первых n членов. Эта формула позволяет получить точное значение суммы при условии, что известны первый элемент прогрессии, знаменатель и количество членов. Однако в некоторых случаях более эффективно использовать другие методы, такие как графическое представление геометрической прогрессии или использование рекуррентных соотношений.
Методы и формулы вычисления суммы первых n чисел геометрической прогрессии
Метод простых множителей:
- Найдите первый элемент геометрической прогрессии;
- Выразите знаменатель прогрессии через первый элемент и сумму первых n элементов;
- Подставьте полученное выражение в формулу для суммы геометрической прогрессии;
- Решите полученное уравнение для нахождения суммы.
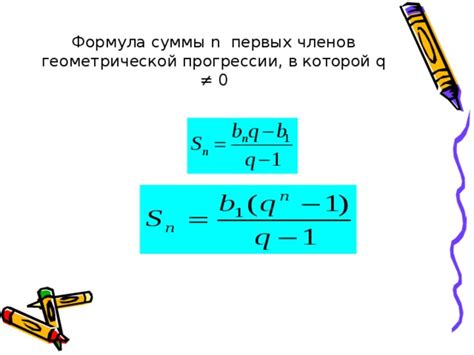
Формула суммы геометрической прогрессии:
Сумма первых n чисел геометрической прогрессии может быть вычислена по следующей формуле:
S = a * (1 - r^n) / (1 - r),
где S - сумма первых n чисел геометрической прогрессии, a - первый элемент прогрессии, r - знаменатель прогрессии, n - количество элементов в прогрессии.
Рекурсивная формула:
Сумма первых n чисел геометрической прогрессии может быть вычислена рекурсивно по следующей формуле:
S(n) = a * (1 - r^n) / (1 - r) + S(n - 1),
где S(n) - сумма первых n чисел геометрической прогрессии, a - первый элемент прогрессии, r - знаменатель прогрессии, S(n - 1) - сумма первых (n - 1) чисел геометрической прогрессии.
Используя эти методы и формулы, можно легко вычислить сумму первых n чисел геометрической прогрессии и использовать ее в различных математических и физических задачах. Это позволяет нам лучше понять свойства и поведение геометрических прогрессий и применять их в реальной жизни.
Методы вычисления суммы геометрической прогрессии
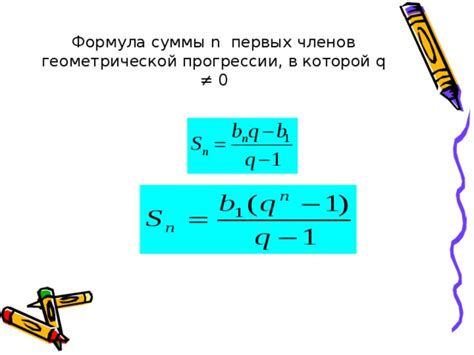
Один из методов - использование формулы для суммы n членов геометрической прогрессии:
Sn = a * (1 - r^n) / (1 - r)
где Sn - сумма первых n членов геометрической прогрессии, a - первый член прогрессии, r - знаменатель прогрессии.
Если знаменатель r меньше 1, то сумма прогрессии имеет конечное значение. Если r равно 1, то каждый член прогрессии равен первому, и сумма будет равна первому члену, умноженному на n. Если r больше 1, то сумма прогрессии будет расти бесконечно.
Еще один метод для вычисления суммы геометрической прогрессии - использование последовательного сложения членов прогрессии:
- Начинаем с первого члена прогрессии и прибавляем к нему второй член;
- К полученной сумме прибавляем третий член;
- Продолжаем этот процесс до тех пор, пока не достигнем n-го члена;
- Получившуюся сумму называем S.
Преимущество этого метода в том, что он не требует использования формулы и может быть применен для вычисления суммы геометрической прогрессии в любых условиях.
Таким образом, существуют различные методы и формулы для вычисления суммы геометрической прогрессии. Выбор определенного метода зависит от вида задачи и доступных данных.
Формулы для вычисления суммы геометрической прогрессии

Сумма первых n членов геометрической прогрессии может быть вычислена с использованием следующей формулы:
Sn = a * (1 - q^n) / (1 - q)
где Sn - сумма первых n членов прогрессии,
a - первый член прогрессии,
q - знаменатель прогрессии,
n - количество членов прогрессии.
Если знаменатель прогрессии равен единице, то формула для вычисления суммы упрощается:
Sn = a * n
Также существует формула для вычисления суммы бесконечно убывающей геометрической прогрессии:
S = a / (1 - q)
где S - сумма бесконечной прогрессии.
Эти формулы позволяют удобно и быстро вычислять сумму геометрической прогрессии без необходимости перебора всех членов последовательности.