Существует ли трапеция с тремя равными сторонами? Геометрия дает ответ!

Геометрия – это древняя наука, занимающаяся изучением фигур, пространственных форм и их свойств. Одним из наиболее интересных объектов, которые изучает геометрия, является трапеция. Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие – нет. Однако, существует ли трапеция, у которой три стороны равны?

На первый взгляд, кажется, что трапеция с тремя равными сторонами невозможна, так как условием трапеции является только параллельность двух сторон. Однако, геометрия может дать нам весьма неожиданный ответ!

Итак, давайте разберемся. Предположим, что у нас есть трапеция ABCD, у которой AC = BC = CD. Такая трапеция была бы, действительно, необычной и отличалась бы от обычных трапеций. Однако, геометрия нас учит, что сумма углов в любом многоугольнике равна 180 градусов. Если вспомнить, что в обычной трапеции угол ADC называется основным, а угол ABC – основополагающим, то в трапеции с равными сторонами углы ADC и ABC были бы одинаковыми. Следовательно, они равны по 90 градусов каждый. Но ведь 90+90=180! Это противоречит законам геометрии, так как сумма углов в траеции не может быть равна 180 градусам. Таким образом, трапеция с тремя равными сторонами не существует!

Существует ли трапеция с тремя равными сторонами?

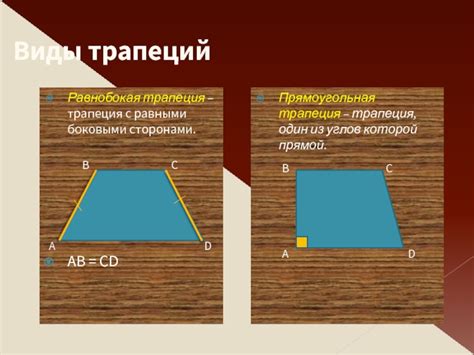
Согласно геометрическим правилам, если трапеция имеет три равные стороны, это означает, что она должна быть равнобедренной. Равнобедренная трапеция - это трапеция, у которой боковые стороны равны, а основания параллельны. Таким образом, центральный угол между сторонами должен быть прямым, а два других угла должны быть равными.

Однако, по определению, у равнобедренной трапеции только две стороны могут быть равными. Третья сторона (основание) всегда отличается от боковых сторон.

Таким образом, ответ на вопрос "Существует ли трапеция с тремя равными сторонами?" - нет, трапеция не может иметь три равные стороны.

Определение трапеции и ее свойства

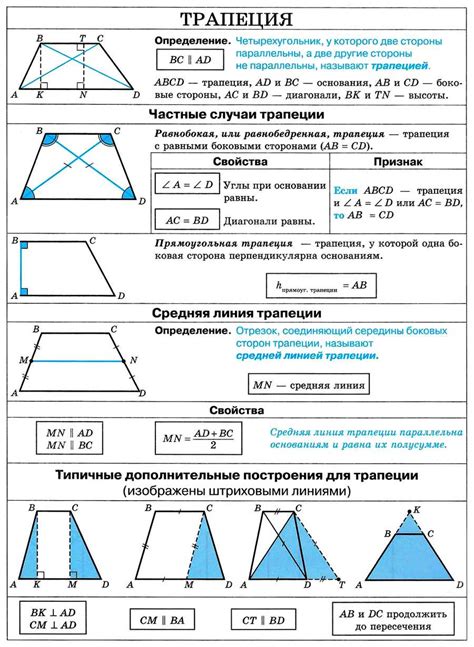
У трапеции есть несколько свойств:

Основания трапеции - параллельные стороны, обозначим их как a и b.
Высота трапеции - расстояние между основаниями, обозначим ее как h.
Боковые стороны трапеции - непараллельные стороны, обозначим их как c и d.
Смежные углы между основаниями и боковыми сторонами трапеции - они являются смежными прилежащими углами.
Противоположные углы трапеции - они являются равными.

Трапеция может быть разделена на два треугольника - верхний и нижний треугольники. Площадь трапеции может быть вычислена по формуле:

S = (a + b) * h / 2

Где a и b - длины оснований, а h - высота трапеции.

Также, для трапеции справедливо следующее равенство:

a + b = c + d

Это свойство позволяет установить равенство суммы длин оснований и суммы длин боковых сторон.

Трапеция может быть разной формы и размера, но важными свойствами каждой трапеции являются параллельность оснований и равенство противоположных углов.

Может ли трапеция иметь три равные стороны?

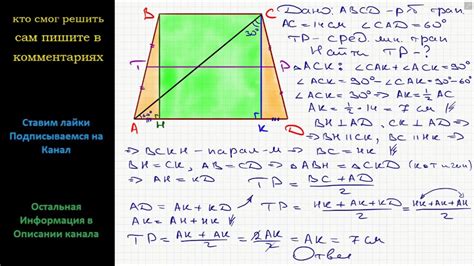
Почему это так? Предположим, что у нас есть трапеция с тремя равными сторонами. Пусть a, b и c будут длинами равных сторон, а d - длина основания трапеции. Так как имеется параллельность между основаниями, то a и b должны быть равны, иначе это не будет трапеция.

Теперь обратим внимание на длину основания d. Если трапеция имеет три равные стороны, то d также должно быть равно a и b. Однако, такое равенство приводит к противоречию, так как основание не может быть одновременно и меньше, и больше двух других сторон. Поэтому, трапеция с тремя равными сторонами не является возможной.

Тем не менее, в геометрии существуют другие специальные четырехугольники, которые могут иметь три равные стороны. Например, ромб - это четырехугольник, у которого все стороны равны. Если вы ищете фигуру с тремя равными сторонами, обратите внимание на ромб, а не трапецию.

Теоремы в геометрии, отвечающие на вопрос

Геометрия, как раздел математики, уделяет особое внимание изучению фигур и их свойств. В ее рамках было разработано много теорем и правил, которые позволяют нам ответить на различные вопросы, связанные с геометрическими фигурами.

В частности, одна такая фигура – трапеция, вызывает интерес. Она имеет две параллельные стороны – основания, и две непараллельные стороны – боковые стороны. Возникает вопрос: существует ли трапеция с тремя равными сторонами?

Ответ – нет. По теореме в геометрии, в трапеции ни одна пара противоположных сторон не может быть равной. Таким образом, в трапеции невозможно найти три равные стороны.

Кроме этой теоремы, существует также ряд других теорем, помогающих нам разобраться с геометрическими фигурами:

Теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Теорема о трех перпендикулярах: всякая прямая, пересекающая две параллельные прямые, образует на них две пары вертикальных углов, равных друг другу.
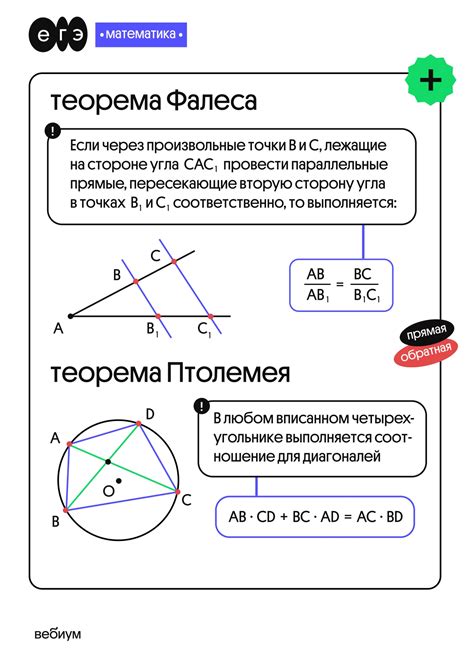
Теорема Фалеса: если две прямые пересекаются с параллельными прямыми, то соответственные отрезки, однородные с ними, пропорциональны.
Теорема о котангенсе: квадрат котангенса угла прямоугольного треугольника равен отношению квадрата катета, противолежащего этому углу, к квадрату гипотенузы.

Это лишь несколько примеров теорем, которые играют важную роль в геометрии и помогают нам понять свойства различных фигур.

Основные примеры и доказательства

Пример 1:

Рассмотрим трапецию ABCD, где AB = BC = CD. Пусть AD - основание трапеции, а AC - боковая сторона. Так как AB = BC = CD, то трапеция ABCD является равнобедренной. Значит, углы A и C равны между собой. Пусть AN и CN - высоты трапеции. Так как трапеция равнобедренная, то высоты AN и CN равны. Следовательно, углы NAD и NCD тоже равны между собой. Получаем, что треугольники NAD и NCD равны по двум сторонам и углу, следовательно, они равны между собой. Это означает, что углы NAD и NAB равны. Но так как AN = CN и ND = NB, то треугольники ANB и CND также равны между собой. Из этого следует, что углы ANB и CND равны. Но ANB и CND - это двугранные углы, которые лежат на одной дуге, значит, их меры равны. Так как ANB + CND = 180°, то каждый из углов равен 90°. Получаем, что трапеция ABCD является прямоугольной трапецией.

Пример 2: