Математика - одна из древнейших наук, и изучение чисел всегда было ее важной частью. В отличие от сложных чисел, простые числа представляют собой целые числа, которые делятся лишь на себя и на 1. Их свойства и закономерности уже давно привлекают внимание математиков.
В этой статье мы рассмотрим таблицу простых чисел до 997 и обсудим особенности и закономерности, связанные с этими числами. Исследуя таблицу, мы сможем увидеть, как простые числа располагаются по порядку и какие числа являются простыми. Такое исследование поможет нам понять общие закономерности и обнаружить интересные факты о простых числах.
Простые числа имеют важное значение в различных областях, включая криптографию и теорию чисел. Исследуя таблицу простых чисел до 997, мы сможем узнать больше о структуре и свойствах этих чисел. Математика продолжает оставаться важной и интересной наукой, и изучение простых чисел является одним из способов расширения наших знаний о мире чисел и их закономерностях.
Первые простые числа
Существует всего 10 первых простых чисел:
- 2 - это наименьшее простое число, которое является единственным четным простым числом.
- 3 - это первое нечетное простое число.
- 5 - это второе нечетное простое число.
- 7 - это третье нечетное простое число.
- 11 - это четвертое нечетное простое число.
- 13 - это пятое нечетное простое число.
- 17 - это шестое нечетное простое число.
- 19 - это седьмое нечетное простое число.
- 23 - это восьмое нечетное простое число.
- 29 - это девятое нечетное простое число.
Эти числа являются основными строительными блоками для построения остальных простых чисел.
Математические методы поиска простых чисел

Один из наиболее известных методов - это метод перебора или "решето Эратосфена". Он заключается в следующем:
- Создается список всех чисел от 2 до заданного предела.
- Берется первое число из списка (2) и помечается как простое.
- Удаляются все числа, кратные этому простому числу.
- Берется следующее непомеченное число в списке и повторяются шаги 2 и 3.
- Процесс продолжается до тех пор, пока все числа не будут проверены.
- Оставшиеся непомеченные числа считаются простыми числами.
Другой метод - это тест Миллера-Рабина, который использует случайность для проверки чисел на простоту. Он имеет некоторую вероятность ошибаться, но при корректном использовании обеспечивает быструю проверку простоты числа.
Также существуют алгоритмы, основанные на разложении чисел на множители, такие как метод Ферма и метод Полларда-Ро).
Таблица простых чисел до 997 может быть создана с использованием одного из этих математических методов. В данном случае, вероятно, использовался метод перебора.
Использование математических методов позволяет не только находить простые числа, но и изучать их особенности и закономерности, а также применять их в различных областях науки и техники.
Особенности простых чисел

Среди особенностей простых чисел можно выделить следующие:
- Бесконечность: простых чисел бесконечное множество. Нет верхней границы, до которой можно перебрать все простые числа.
- Разреженность: простые числа распределены по числовой оси неравномерно. Между любыми двумя последовательными простыми числами может быть много составных чисел.
- Сложность факторизации: разложение составного числа на простые множители является сложной задачей. Для больших чисел факторизация может потребовать значительного вычислительного времени.
- Использование в криптографии: простые числа играют важную роль в современной криптографии, особенно в алгоритмах шифрования и аутентификации.
- Закономерности: существуют некоторые математические закономерности и свойства простых чисел, такие как теорема о бесконечности простых чисел и теорема Вильсона.
Изучение особенностей простых чисел позволяет лучше понять и использовать их в различных областях, таких как математика, компьютерные науки и криптография.
Простые числа в таблице до 997

Такая таблица позволяет легко и быстро найти все простые числа до 997 без необходимости выполнять вычисления. Она является полезным инструментом не только для математиков, но и для программистов, которым требуется использовать простые числа в своих проектах.
В таблице можно наблюдать некоторые закономерности и особенности, характерные для простых чисел. Например, все простые числа, кроме двойки, являются нечетными. Также простые числа расположены неравномерно: они чаще встречаются ближе к нулю, и их количество уменьшается по мере увеличения числа.
Использование таблицы простых чисел до 997 может значительно ускорить процесс поиска простых чисел и помочь найти особенности и закономерности, связанные с этими числами.
Пример небольшой части таблицы:
| Число | Простое? |
| 2 | Да |
| 3 | Да |
| 5 | Да |
| 7 | Да |
| 11 | Да |
Таким образом, таблица простых чисел до 997 представляет собой полезный инструмент для исследования простых чисел и их особенностей.
Закономерности и особенности таблицы простых чисел
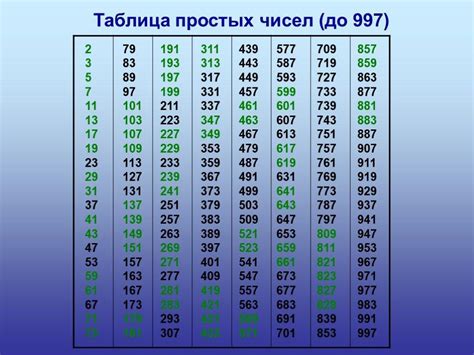
Таблица простых чисел до 997 представляет собой важный инструмент для исследования и анализа числовых последовательностей. В ней можно найти множество закономерностей и особенностей, которые позволяют лучше понять природу простых чисел.
Одна из основных закономерностей, которую можно наблюдать в таблице простых чисел, это их распределение. Простые числа не являются равномерно распределенными по всему числовому ряду, они скапливаются в определенных интервалах и редко встречаются в других. Например, в таблице можно заметить, что некоторые интервалы между простыми числами содержат больше чисел, чем другие.
Также в таблице простых чисел можно обнаружить определенные закономерности в их последовательности. Например, простые числа часто имеют вид 6n ± 1, где n - натуральное число. Это наблюдение было сделано Эратосфеном и носит название "формула Эратосфена".
Еще одна интересная особенность таблицы простых чисел до 997 заключается в их связи с другими математическими концепциями. Например, простые числа широко используются в криптографии, так как служат основой многих алгоритмов шифрования. Кроме того, простые числа играют важную роль в теории чисел, анализе алгоритмов и многих других областях математики.
Распределение простых чисел в таблице
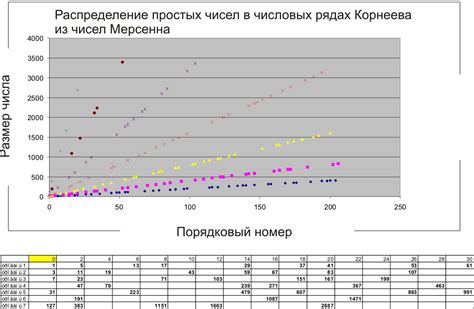
Как мы движемся по строкам таблицы, можно заметить, что простые числа часто чередуются с составными числами. Эта закономерность можно наблюдать в столбцах таблицы. Например, второй столбец содержит простые числа, третий - составные, четвертый - простые и так далее. Такое чередование создает интересную геометрическую симметрию в распределении простых чисел.
Еще одной интересной особенностью распределения простых чисел в таблице является их сгустки. Обратим внимание на то, что простые числа, расположенные рядом, имеют близкие значения и окончания. Это можно наблюдать, например, в третьем столбце, где простые числа имеют значения 3, 13, 23, 43 и т.д. Такое сгущение простых чисел указывает на то, что они не являются равномерно распределенными по всей таблице, а скорее сконцентрированы в некоторых областях.
Итак, распределение простых чисел в таблице отображает их уникальные закономерности и особенности. Чередование с составными числами, окончания на 1, 3, 7 и 9, сгустки значений - все это придает простым числам особый характер. Изучение этих закономерностей помогает нам лучше понять и описывать их свойства.
Особенности последовательности простых чисел

Одной из особенностей последовательности простых чисел является их бесконечное количество. Это означает, что не существует наибольшего простого числа и все время можно найти новые простые числа, если продолжать искать.
Другой интересной особенностью простых чисел является их распределение по числовой прямой. Нет простого правила или формулы, которая может точно предсказать, где будет находиться следующее простое число. Это делает их распределение неопределенным и сложным для анализа.
Несмотря на сложность распределения, существуют некоторые закономерности и особенности в последовательности простых чисел. Например, известно, что все простые числа, кроме 2, являются нечетными числами. Также известно, что простые числа, большие 2, не могут быть кратны другим простым числам.
Еще одна интересная особенность простых чисел связана с их использованием в криптографии. Простые числа играют важную роль в системах шифрования, где они используются для создания секретных ключей и защиты информации.
Исследование особенностей и закономерностей простых чисел является актуальной темой для математических исследований, и может иметь практическое применение в различных областях, включая компьютерную науку и криптографию.



