Таблица умножения - это неотъемлемый инструмент в математике, который помогает визуализировать взаимосвязь между числами и их произведениями. В языке программирования Python существуют различные способы создания таблицы умножения, и одним из них является использование цикла while.
Цикл while - это конструкция, которая позволяет выполнять определенный набор инструкций до тех пор, пока условие цикла истинно. В случае таблицы умножения, мы можем использовать цикл while для генерации всех возможных произведений чисел от 1 до 10.
После того, как мы написали код для таблицы умножения, мы можем его запустить и увидеть результат. Например, таблица умножения числа 5 будет выглядеть следующим образом:
Основные принципы работы таблицы умножения в Python через while
Основная идея работы таблицы умножения в Python через цикл while заключается в следующих принципах:
- Устанавливаем начальное значение переменных, которые будут использоваться для вычисления.
- Проверяем условие, которое определяет, должен ли цикл продолжаться или нет.
- Затем изменяем значения переменных в соответствии с логикой таблицы умножения: увеличиваем счетчик строки и проверяем, достигли ли мы конца таблицы.
- Повторяем шаги 2-4 до тех пор, пока условие не станет ложным.
Это основное устройство цикла while при создании таблицы умножения в Python. Управление циклом происходит в соответствии с условием, что позволяет эффективно генерировать таблицы умножения любого размера.
Примеры умножения числа на другие числа с помощью цикла while
Пример:
# Задаем число, с которым будем умножать
num = 5
# Задаем счетчик, с которого начнется умножение
i = 1
# Пока счетчик меньше или равен 10
while i
result = num * i
print(f"{num} * {i} = {result}")
# Увеличиваем счетчик на 1
i += 1
Выполнение этого кода выведет таблицу умножения числа 5 на числа от 1 до 10:
5 * 1 = 5
5 * 2 = 10
5 * 3 = 15
5 * 4 = 20
5 * 5 = 25
5 * 6 = 30
5 * 7 = 35
5 * 8 = 40
5 * 9 = 45
5 * 10 = 50
Таким образом, используя цикл while вместе с операцией умножения, можно легко создавать таблицы умножения для различных чисел.
Объяснение работы цикла while в таблице умножения
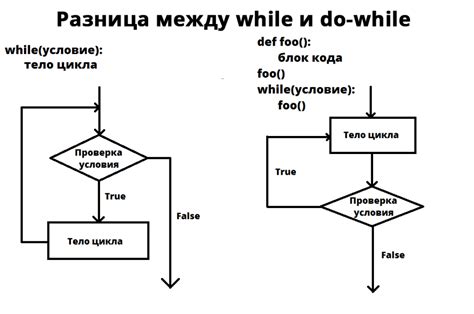
Основная идея работы цикла while заключается в том, что он выполняет код, пока условие истинно. Кода внутри цикла будет выполняться до тех пор, пока заданное условие остается верным. Как только условие становится ложным, выполнение цикла останавливается и программа продолжает работу со следующей инструкцией после цикла.
При создании таблицы умножения, первый цикл while используется для итерации от 1 до 10 и задает значение текущего числа, от которого будут производиться умножения. Во втором вложенном цикле while, производится итерация от 1 до 10 и задается значение текущего числа, на которое будет умножаться первое число.
Применение условия остановки в таблице умножения через while
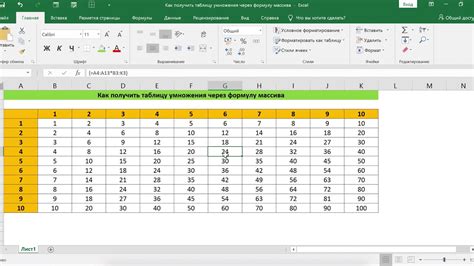
В Python, чтобы создать таблицу умножения через цикл while, можно использовать условие остановки. Условие остановки позволяет контролировать количество операций умножения и закончить цикл при достижении определенного множителя.
Например, если мы хотим создать таблицу умножения для числа 5 до множителя 10, мы можем использовать цикл while с условием остановки:
multiplicand = 5
multiplier = 1
while multiplier Применение условия остановки позволяет гибко контролировать количество операций умножения в таблице. Мы можем легко изменить множитель, добавить дополнительные условия или изменить предел для цикла.
Решение задачи на таблицу умножения через while
Для решения задачи на таблицу умножения с использованием цикла while, мы можем создать два вложенных цикла while, которые будут перебирать значения от 1 до заданного числа. Первый цикл будет отвечать за множитель, а второй цикл будет отвечать за множимое.
Код для решения задачи на таблицу умножения через while может выглядеть следующим образом:
x = 1
while xТаким образом, при выполнении данного кода мы получим таблицу умножения от 1 до 10, где результаты умножения отделяются символами табуляции.