Тангенс – это одна из основных тригонометрических функций, которая является отношением противолежащего катета к прилежащему катету. В мире математики тангенс треугольника занимает важное место, так как позволяет определить углы и стороны треугольника с помощью известных значений.
Значение тангенса может быть как положительным, так и отрицательным, в зависимости от положения угла в треугольнике. Если угол лежит в первой или третьей четверти, то тангенс будет положительным, а если угол лежит во второй или четвертой четверти, то тангенс будет отрицательным.
Тангенс также имеет свойства, которые помогают в решении различных геометрических и физических задач. Например, тангенс суммы двух углов можно выразить через тангенсы этих углов, а также через синусы и косинусы. Это свойство позволяет упростить вычисления и упрощает решение сложных задач.
Что такое тангенс треугольника?
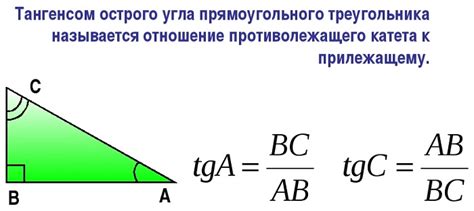
Значение тангенса треугольника может быть вычислено как отношение синуса угла треугольника к косинусу этого угла. Математически это выражается следующей формулой:
| Тригонометрическая функция | Формула |
|---|---|
| Тангенс треугольника | тангенс α = sin α / cos α |
Значение тангенса треугольника может быть положительным или отрицательным, в зависимости от квадранта, в котором находится конечная точка луча, соответствующего заданному углу треугольника.
Тангенс треугольника широко используется в различных областях науки и инженерии, таких как физика, геометрия, электротехника и многих других. Он позволяет вычислять углы треугольников и решать различные задачи, связанные с их геометрией.
Определение, значение и основные свойства

Значение тангенса треугольника может быть представлено числом, которое показывает, насколько высока противоположная сторона треугольника по сравнению с прилежащей стороной.
Основные свойства тангенса треугольника:
| Значение | Свойство |
| 0 | Тангенс равен нулю, когда противоположная сторона равна нулю или когда прилежащая сторона равна бесконечности. |
| 1 | Тангенс равен единице, когда противоположная сторона равна прилежащей стороне. |
| Бесконечность | Тангенс равен бесконечности, когда противоположная сторона равна бесконечности или когда прилежащая сторона равна нулю. |
| Положительное число | Тангенс положителный, когда противоположная сторона и прилежащая сторона имеют одинаковый знак. |
| Отрицательное число | Тангенс отрицательный, когда противоположная сторона и прилежащая сторона имеют противоположный знак. |
Применение тангенса треугольника

- Геометрия. Тангенс треугольника используется для нахождения углов и сторон треугольника при известной длине одной стороны и известных углах. Это позволяет решать задачи по геодезии, строительству и другим геометрическим дисциплинам.
- Физика. Тангенс треугольника используется для решения задач в механике, оптике, гидродинамике и других физических науках. Например, он позволяет определить угол падения светового луча на границе двух сред, угол наклона плоскости наклона и т. д.
- Инженерия. Тангенс треугольника используется при проектировании и конструировании различных механизмов, машин и сооружений. Он позволяет определить угол наклона поверхности плоскости, оптимальный угол наклона для обеспечения максимальной силы трения и многие другие параметры.
- Радиофизика и электроника. Тангенс треугольника используется при расчете и проектировании антенн, фильтров, усилителей и других радиоэлектронных устройств. Он позволяет определить угол наклона антенны, угол наклона плоскости поляризации и другие характеристики сигнала.
- Математика. Тангенс треугольника является основой для построения тангенциальной системы мер и единиц углов. Он также используется в различных математических моделях для решения задач оптимизации, аппроксимации функций и других вычислительных задач.
Таким образом, знание тангенса треугольника и его применение позволяют решать разнообразные задачи в различных научных и инженерных областях.
Как применять тангенс для решения задач
Одним из самых распространенных способов использования тангенса является нахождение значения неизвестного угла. Для этого необходимо знать значения двух известных сторон треугольника и применить соответствующую формулу.
Например, пусть у нас есть прямоугольный треугольник, в котором известны значения катета и гипотенузы. Чтобы найти значение неизвестного угла, мы можем воспользоваться формулой:
тангенс угла = противоположная сторона / прилежащая сторона
Подставив известные значения, мы сможем выразить тангенс угла и найти его численное значение.
Также, тангенс может использоваться для нахождения значений неизвестных сторон треугольника. В этом случае известны значения углов и одной из сторон. После нахождения тангенса угла, мы можем выразить неизвестную сторону через известные и найденный угол.
Важно помнить, что в некоторых случаях тангенс может иметь бесконечное значение или быть неопределенным. Например, если значение угла равно 90 градусов, тангенс будет неопределенным, так как деление на ноль невозможно.
Таким образом, тангенс является мощным инструментом в решении различных задач, требующих вычислений в треугольниках и связанных с тригонометрией. Он позволяет находить значения сторон и углов, а также решать более сложные задачи с использованием соответствующих формул и уравнений.
Формулы и связи тангенса с другими тригонометрическими функциями

Тангенс угла α может быть выражен через синус и косинус этого угла:
tg(α) = sin(α) / cos(α)
Обратная функция тангенса называется арктангенс (или арктангенсус). Арктангенс обозначается как arctg или atan.
Среди основных свойств тангенса треугольника можно выделить:
- Тангенс принимает все положительные и отрицательные значения, включая нуль.
- Функция тангенс является нечетной.
- Если тангенс угла равен единице, то сам угол равен 45 градусам или π/4 радиан.
Связь тангенса с другими тригонометрическими функциями позволяет нам использовать его в решении различных задач и применять в математических и физических расчетах.