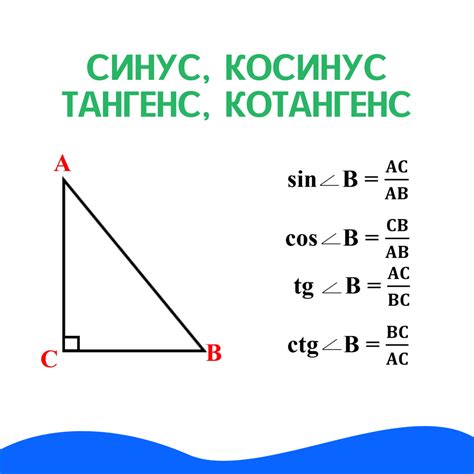
Тангенс угла - одна из основных тригонометрических функций, которая широко используется в математике и физике. Она позволяет нам вычислять отношение величины противолежащего катета к прилежащему катету прямоугольного треугольника.
Формула для вычисления тангенса угла проста: тангенс угла равен отношению противолежащего катета к прилежащему катету:
tg(α) = противолежащий катет / прилежащий катет
Тангенс угла может быть представлен также как отношение синуса косинуса:
tg(α) = sin(α) / cos(α)
Пример нахождения тангенса угла:
Пусть имеется прямоугольный треугольник со сторонами a = 3 и b = 4. Мы хотим найти тангенс угла α.
Сначала найдем значение синуса и косинуса угла α:
sin(α) = противолежащий катет / гипотенуза = 3 / 5 = 0.6
cos(α) = прилежащий катет / гипотенуза = 4 / 5 = 0.8
Теперь мы можем вычислить значение тангенса угла α:
tg(α) = sin(α) / cos(α) = 0.6 / 0.8 = 0.75
Таким образом, тангенс угла α равен 0.75.
Тангенс угла: основная формула и примеры расчетов
| Тангенс угла | = | Противолежащий катет | ÷ | Прилежащий катет |
|---|---|---|---|---|
| tg(α) | = | a | ÷ | b |
Здесь α - угол, a - длина противолежащего катета, b - длина прилежащего катета.
Примеры расчетов тангенса угла:
1. Дан прямоугольный треугольник, в котором противолежащий катет равен 4, а прилежащий катет равен 3. Найдем тангенс угла α.
| tg(α) | = | 4 | ÷ | 3 | = | 1.333 |
Ответ: tg(α) ≈ 1.333
2. В прямоугольном треугольнике известны катеты: противолежащий - 6, прилежащий - 8. Найдем тангенс угла β.
| tg(β) | = | 6 | ÷ | 8 | = | 0.75 |
Ответ: tg(β) = 0.75
Таким образом, тангенс угла позволяет находить отношение противолежащего и прилежащего катетов в прямоугольном треугольнике и может быть использован для решения различных задач в геометрии и физике.
Определение и особенности тангенса
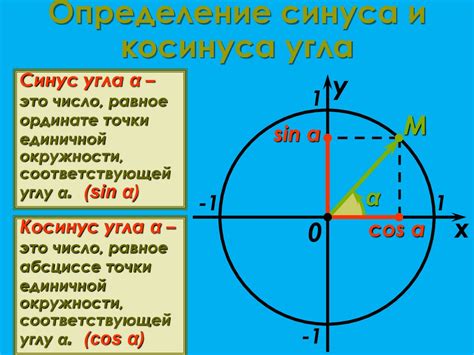
Особенности тангенса:
- Тангенс угла может быть определен только для прямоугольных треугольников.
- Значение тангенса может быть отрицательным, положительным или равным нулю в зависимости от расположения угла относительно осей координат.
- Тангенс угла может быть представлен как дробью, целым числом или десятичной дробью.
- Значение тангенса увеличивается с увеличением угла от 0° до 90°, достигая бесконечности при угле 90°.
Тангенс угла широко используется в математике, физике и других науках для решения задач, связанных с углами и треугольниками. Знание особенностей тангенса позволяет проводить точные вычисления и анализировать углы и треугольники с высокой точностью.
Как найти тангенс угла в прямоугольном треугольнике
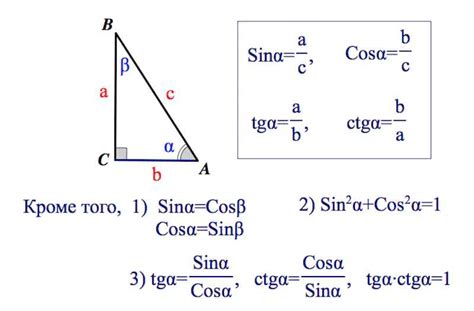
Тангенс угла в прямоугольном треугольнике определяется как отношение противоположного катета к прилежащему катету. Для его вычисления можно использовать основную формулу: тангенс угла равен отношению противоположнего катета к прилежащему катету.
Для нахождения тангенса угла необходимо знать значения противоположнего и прилежащего катетов. Первым шагом нужно определить значения этих катетов в треугольнике. После этого можно применить формулу и вычислить тангенс угла.
Например, если в прямоугольном треугольнике противоположний катет равен 6, а прилежащий катет равен 4, то тангенс угла можно найти следующим образом: тангенс угла = 6 / 4 = 1.5.
Таким образом, тангенс угла в прямоугольном треугольнике можно найти, используя значение противоположного и прилежащего катетов. Это позволяет определить угол и использовать его значения в дальнейших вычислениях или приложениях.
Примеры расчета тангенса угла
Для нахождения значения тангенса угла необходимо разделить значение синуса угла на значение косинуса угла.
Пример 1:
Рассмотрим прямоугольный треугольник со сторонами a = 3 и b = 4.
Для нахождения значения тангенса угла А можно воспользоваться формулой:
tg(A) = a / b
tg(A) = 3 / 4 = 0.75
Пример 2:
Пусть дан треугольник АВС, в котором известны сторона AB = 5 и угол BAC = 30°.
Для нахождения значения тангенса угла BAC можно воспользоваться формулой:
tg(BAC) = BC / AB
Так как угол BAC = 30° и сторона AB = 5, значение BC можно найти, используя формулу:
BC = AB * tg(BAC)
BC = 5 * 0.577 = 2.885
Таким образом, tg(BAC) = 2.885 / 5 = 0.577
Пример 3:
Пусть дан треугольник XYZ, в котором известны сторона YZ = 7 и угол ZYX = 60°.
Для нахождения значения тангенса угла ZYX можно воспользоваться формулой:
tg(ZYX) = YX / YZ
Так как угол ZYX = 60° и сторона YZ = 7, значение YX можно найти, используя формулу:
YX = YZ * tg(ZYX)
YX = 7 * 1.732 = 12.124
Таким образом, tg(ZYX) = 12.124 / 7 = 1.732
Практическое применение тангенса угла

Ниже приведены несколько примеров, где тангенс угла может быть использован для решения практических задач:
- Инженерное строительство: Тангенс угла может использоваться для определения высоты недоступных объектов. Используя тангенс угла между наблюдателем и вершиной объекта, инженеры могут рассчитать высоту объекта, используя известную длину основания и значение тангенса.
- Навигация: Тангенс угла используется в навигационных системах для определения расстояния и направления. Используя тангенс угла между направлением движения и признаком на местности, навигационные устройства могут рассчитать необходимые данные для навигации.
- Физика: Тангенс угла может быть использован для решения задач в физике, связанных с механикой тела. Например, в задачах на механику движения тела по наклонной плоскости, тангенс угла наклона плоскости может быть использован для определения силы трения и ускорения тела.
- Математика: Тангенс угла широко используется в математике при решении уравнений, графиков и теорем. Он может использоваться для нахождения значений углов в треугольниках или для решения геометрических задач.
- Телекоммуникации: Тангенс угла может быть использован для определения угла наклона антенн при развертывании телекоммуникационных систем. Зная значение тангенса угла наклона антенны и расстояние до цели, можно точно настроить антенну для передачи и приема сигналов.
Тангенс угла имеет множество практических применений и играет важную роль в различных областях. Понимание и использование этого тригонометрического соотношения позволяет решать множество задач и улучшать качество работы в различных профессиональных сферах.