Построение поверхности, заданной уравнением, может быть сложной и захватывающей задачей для любого любителя математики. В данной статье мы рассмотрим подробное руководство по этому процессу, которое поможет вам разобраться в основных шагах и принципах создания таких поверхностей. Важно отметить, что в основе этого процесса лежит знание математического аппарата и навыки работы с уравнениями.
Первый шаг в построении поверхности - понять уравнение, которое задает эту поверхность. В основном, уравнение может иметь вид функции двух переменных или трехмерное уравнение, включающее три переменные. Для примера, мы рассмотрим уравнение поверхности с функцией двух переменных: z = f(x, y), где z - это высота, а x и y - координаты точки на плоскости. Обратите внимание, что функцию f можно взять известной функцией или создать ее самостоятельно.
Второй шаг - определить диапазоны значений для x и y, в пределах которых вы хотите построить поверхность. Обычно это оговаривается в условиях задачи или согласно требованиям построения. Затем выбирается определенное количество точек внутри этого диапазона, через которые будет проходить поверхность. Чем больше точек выберешь, тем более детализированной будет поверхность. Лучше начать с малого количества точек и увеличить их число по мере необходимости.
Третий шаг - вычислить значения высоты z для каждой выбранной точки на плоскости, используя функцию f и координаты x и y. Это позволит вам найти третью компоненту каждой точки, которая определит высоту на поверхности.
Продолжая эти вычисления для всех выбранных точек и соединяя их, вы получите поверхность, заданную уравнением. Чтобы визуализировать полученную поверхность, можно использовать математическое программное обеспечение, такое как MATLAB, Python с библиотеками matplotlib и NumPy, либо другие инструменты визуализации данных. Это позволит вам получить графическое представление исходной поверхности, которая может быть проанализирована и изучена дальше.
Важно отметить, что построение поверхности, заданной уравнением, требует определенных навыков математики и программирования. В зависимости от сложности уравнения и требуемой детализации, этот процесс может быть более или менее сложным. Однако, с помощью правильного подхода и упорства, вы сможете создать потрясающие и визуально привлекательные поверхности.
Определение поверхности и ее уравнение
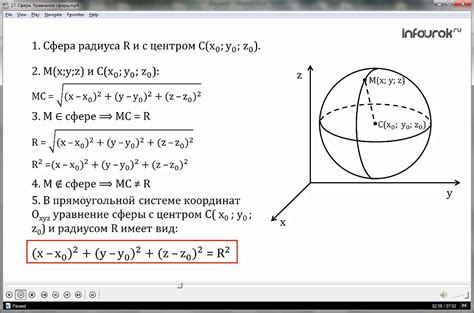
Уравнение поверхности служит для описания геометрических свойств объекта. Оно представляет собой математическую формулу, связывающую координаты точек на поверхности с их характеристиками, такими как цвет, высота, температура и т. д.
Уравнение поверхности может быть задано в явном или неявном виде. В явном виде уравнение позволяет явно выразить одну переменную через остальные, например, y = f(x, z). В неявном виде уравнение определяет поверхность в виде связи между всеми переменными, например, F(x, y, z) = 0.
Примеры:
- Уравнение плоскости: Ax + By + Cz + D = 0, где A, B, C и D - коэффициенты.
- Уравнение сферы: (x - a)^2 + (y - b)^2 + (z - c)^2 = r^2, где (a, b, c) - координаты центра, r - радиус.
Зная уравнение поверхности, можно проводить различные геометрические и аналитические операции, такие как нахождение точек пересечения с другими поверхностями, определение кривизны в заданной точке, вычисление площади и объема, а также создание компьютерных моделей и визуализацию объектов.
Значение и применение поверхностей в математике

Одним из основных применений поверхностей в математике является их использование для моделирования физических объектов. Например, при анализе и проектировании инженерных конструкций, таких как мосты, здания или самолеты, их форма и поверхность могут быть представлены математическими уравнениями. Это позволяет инженерам и архитекторам проводить более точные расчеты и предсказывать поведение объектов в различных условиях.
Поверхности также играют важную роль в физике. Например, они используются для описания электромагнитных полей, распределения температуры, световых потоков и других физических величин. Математические уравнения, описывающие поверхности, позволяют ученым исследовать различные физические процессы и разрабатывать новые технологии.
Кроме того, поверхности имеют важное значение в геометрии. Изучение и классификация различных типов поверхностей позволяет ученым разрабатывать новые геометрические модели, решать сложные геометрические задачи и исследовать свойства различных фигур и пространств.
Классификация поверхностей
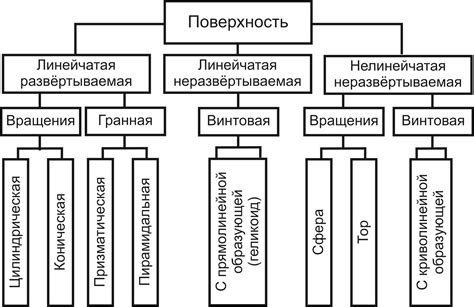
Поверхности могут быть классифицированы на основе различных характеристик. Некоторые из основных категорий поверхностей включают:
| Тип поверхности | Описание |
|---|---|
| Плоскость | Поверхность, которая является плоской и не имеет кривизны. |
| Цилиндр | Поверхность, которая имеет форму цилиндра. |
| Конус | Поверхность, которая имеет форму конуса. |
| Сфера | Поверхность, которая имеет форму сферы. |
| Тор | Поверхность, которая имеет форму тора. |
| Параболоид | Поверхность, которая имеет форму параболоида. |
| Эллипсоид | Поверхность, которая имеет форму эллипсоида. |
| Гиперболоид | Поверхность, которая имеет форму гиперболоида. |
Это лишь некоторые из возможных типов поверхностей, которые можно построить на основе их уравнений. Знание классификации поверхностей поможет в понимании и разработке подходящих методов и алгоритмов для их построения.
Конструирование поверхности
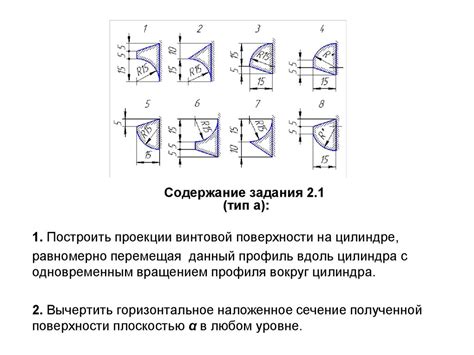
Для того чтобы построить поверхность, заданную уравнением, следуйте данному руководству:
- Шаг 1: Определите уравнение поверхности. Убедитесь, что у вас есть явное или неявное уравнение, описывающее поверхность.
- Шаг 2: Определите диапазоны значений переменных. Узнайте, в каких пределах изменяются переменные в уравнении. Это поможет вам определить, какую область поверхности следует построить.
- Шаг 3: Разделите продолжение на множество точек. Для построения поверхности вам нужно разбить заданный диапазон переменных на равные или неравные интервалы.
- Шаг 4: Замените значения переменных в уравнении и решите его для каждой точки. Полученные значения будут определять высоту или координаты z-оси для каждой точки поверхности.
- Шаг 5: Постройте точки на плоскости с использованием найденных координат. Соедините эти точки, чтобы получить поверхность. Можно использовать 3D-программное обеспечение или математические графические пакеты для этого.
- Шаг 6: Проверьте результат. Убедитесь, что построенная поверхность соответствует вашему уравнению. Проверьте также, что вы обошли все значения переменных.
Следуя этим шагам, вы сможете построить поверхность, заданную уравнением, и визуализировать ее для дальнейшего анализа и изучения.
Шаги в процессе построения поверхности

Построение поверхности, заданной уравнением, может быть разделено на несколько этапов. Для того чтобы успешно построить поверхность, следует следовать следующим шагам:
| Шаг 1: | Определить уравнение поверхности. Для этого нужно знать, какие переменные задействованы в уравнении и как они взаимосвязаны. Например, уравнение может иметь вид z = f(x, y), где z - высота поверхности, а x, y - координаты на плоскости. |
| Шаг 2: | Определить диапазоны значений переменных. Это позволит определить область, в которой будет происходить построение поверхности. |
| Шаг 3: | Создать сетку точек. На этом шаге осуществляется разбиение заданной области на сегменты и определение значений переменных для каждой точки. Это поможет задать сетку точек, которые будут использоваться для построения поверхности. |
| Шаг 4: | Вычислить значение функции в каждой точке сетки. На этом шаге происходит вычисление значений функции f(x, y) для каждой точки сетки. Полученные значения будут определять высоту поверхности в каждой точке. |
| Шаг 5: | Построить поверхность. На этом последнем шаге использование найденных значений функции и координат точек сетки позволяет построить поверхность. Визуализацию можно выполнить с помощью графической библиотеки или специализированного программного обеспечения. |
Следуя этим шагам, можно успешно построить поверхность, заданную уравнением, и визуализировать ее в трехмерном пространстве.
Использование математических уравнений для моделирования поверхности
Одним из наиболее распространенных методов создания 3D-поверхностей является использование уравнений. Это позволяет точно определить форму и свойства объектов, таких как горы, океаны, здания и т. д. В основе этого метода лежит преобразование математических уравнений в точки, которые затем соединяются и образуют поверхность.
Одним из примеров использования математических уравнений для построения поверхностей является уравнение сферы:
- Уравнение сферы:
(x - a)^2 + (y - b)^2 + (z - c)^2 = r^2 (a, b, c)- координаты центра сферыr- радиус сферы
Для построения сферы можно использовать математический пакет, такой как MATLAB или Python с библиотекой Matplotlib. С помощью этих инструментов можно задать значания a, b, c и r, а затем сгенерировать точки на поверхности сферы.
Кроме того, математические уравнения могут использоваться для моделирования более сложных форм, таких как тор, эллипсоид, куб и другие. Для каждой формы существуют соответствующие уравнения, которые можно использовать для их построения и визуализации.
Использование математических уравнений для моделирования поверхностей позволяет создавать реалистичные 3D-модели с высокой точностью. Этот метод широко применяется в различных областях, включая компьютерную графику, научное моделирование и инженерное проектирование.
Инструменты и программы для построения поверхности
1. Mathematica:
Mathematica - одна из самых популярных программ для математических вычислений и построения графиков. В ней можно использовать различные функции и уравнения для создания трехмерных поверхностей. Mathematica предоставляет широкие возможности для добавления визуальных элементов, изменения масштаба, добавления цветовой палитры и многое другое.
2. MATLAB:
MATLAB - программное обеспечение для математических вычислений и научного моделирования. Он содержит мощный инструментарий для работы с трехмерными графиками и поверхностями. MATLAB позволяет задавать функции и уравнения, задавать параметры визуализации и редактировать графики в реальном времени.
3. GeoGebra:
GeoGebra - бесплатная программа для математических вычислений и создания графиков. Она имеет простой и интуитивно понятный интерфейс, что делает ее доступной даже для начинающих пользователей. В GeoGebra можно использовать функции и уравнения для построения трехмерных поверхностей, регулировать параметры, включать анимацию и многое другое.
4. Blender:
Blender - программное обеспечение для трехмерного моделирования и создания анимации. Она позволяет создавать сложные трехмерные объекты и эффекты, включая поверхности. Blender предлагает множество инструментов для моделирования, настройки освещения, добавления материалов и создания анимации, что делает ее полезной для создания реалистичных трехмерных поверхностей.
5. Wolfram Alpha:
Wolfram Alpha - онлайн-сервис, предоставляющий вычислительную информацию и графические данные. В нем можно использовать уравнения и функции для построения графиков и поверхностей. Wolfram Alpha позволяет задавать параметры визуализации, менять масштаб, добавлять аннотации и многое другое. Он также предоставляет дополнительные инструменты для анализа и работы с построенными поверхностями.
Выбор инструмента или программы для построения поверхности зависит от ваших потребностей, навыков и предпочтений. У каждой из этих программ есть свои особенности и возможности, поэтому стоит попробовать несколько из них, чтобы найти наиболее подходящую для вас.