Соединение точек из разных плоскостей – это одна из самых важных задач в графическом дизайне и иллюстрациях. Эта техника позволяет создать сложные композиции, добавляя глубину и перспективу к изображению. Существует несколько методов для соединения точек разных плоскостей, каждый из которых имеет свои особенности и применяется в различных ситуациях.
Один из методов соединения точек из разных плоскостей - использование линейной перспективы. Эта техника основывается на принципе, что параллельные линии в глубине сходятся в одной точке – исчезающей точке. Чтобы создать эффект глубины, линии, ведущие вглубь изображения, рисуются с повышенной точностью и учитываются законы перспективы.
Другой метод соединения точек из разных плоскостей – это использование цветовой перспективы. Цвета в дальних плоскостях изображения становятся более бледными, менее насыщенными, что создает ощущение глубины и пространства. Практически можно передать переход от одной плоскости к другой при помощи изменения цветовых оттенков или добавления градиентов.
Также существуют методы соединения точек из разных плоскостей через использование геометрических фигур или текстур. Умелое сочетание фигур и текстур позволяет создать ощущение объемности и глубины в изображении, а также подчеркнуть центральные элементы и привлечь внимание зрителя.
Метод совмещения координат
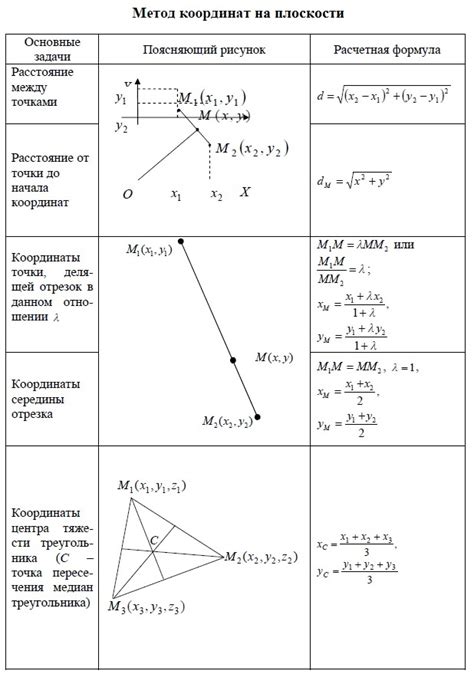
Для применения метода совмещения координат необходимо:
- Определить точки, которые требуется соединить.
- Разбить точки на группы, в зависимости от их координат.
- Выделить главные точки, которые будут служить опорными при соединении.
- Произвести переход от одной плоскости к другой, используя общие или близкие координаты главных точек.
- Соединить точки по полученным координатам, создавая плавные линии и контуры объекта.
Применение метода совмещения координат позволяет создать композицию, в которой точки визуально связаны и расположены гармонично. Этот метод особенно полезен при создании графических иллюстраций, логотипов, дизайна интерьера и других проектов, требующих точного соединения элементов.
Пример использования метода совмещения координат:
- В качестве главных точек выбраны углы прямоугольника.
- На другой плоскости выбраны точки, которые имеют соответствующие или близкие координаты по отношению к главным точкам прямоугольника.
- Соединение точек осуществляется по полученным координатам, создавая плавные линии и общий контур фигуры.
Таким образом, метод совмещения координат позволяет создавать сложные и визуально привлекательные композиции, объединяющие элементы разных плоскостей и подчеркивающие их гармонию.
Метод проецирования на плоскость
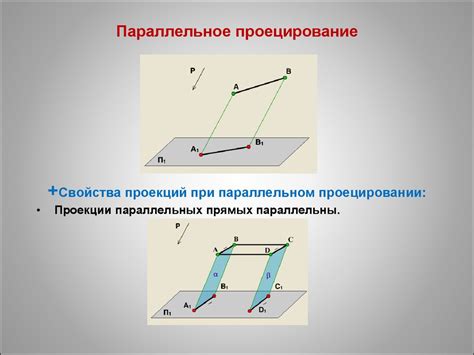
Основная идея метода проецирования на плоскость заключается в том, чтобы преобразовать трехмерные координаты точек в двумерные координаты на плоскости проекции. Для этого используется математическое преобразование, которое основано на разных моделях проецирования, таких как перспективная проекция, ортографическая проекция и т. д.
Перспективная проекция является одной из наиболее распространенных моделей проецирования на плоскость. Она представляет собой модель, которая позволяет учитывать перспективу и создавать трехмерное впечатление на плоском изображении. Однако, она имеет свои ограничения и может приводить к искажениям при отображении далеко удаленных объектов.
Ортографическая проекция, в свою очередь, является моделью проецирования, при которой параллельные лучи света проходят через фокусное отверстие камеры. Такая модель не учитывает перспективу и не создает искажений при отображении далеких объектов. Она полезна для создания технических чертежей и схем, где важна точность и пропорциональность изображения.
В итоге, метод проецирования на плоскость является важным инструментом в компьютерной графике и визуализации. Он позволяет создавать реалистичные трехмерные модели и изображения, которые могут быть представлены на двумерных экранах или печатных носителях, что делает его неотъемлемой частью различных сфер деятельности, таких как архитектура, медицина, игровая индустрия и дизайн.
Метод использования соединительных линий
Для использования соединительных линий возможно применение следующих методов:
- Метод прямой линии. Этот метод подразумевает простое соединение точек линией без использования сложных геометрических фигур. Он особенно полезен при представлении последовательности действий или эволюции процесса.
- Метод обычной кривой линии. В этом методе используется кривая линия, пролегающая через заданные точки. Она может быть использована для создания более сложных связей и наглядного представления данных.
- Метод пунктирной линии. Пунктирная линия может использоваться для указания временных или условных связей между точками. Она создает эффект "нескольких вариантов" или "возможен/невозможен".
Примеры использования соединительных линий включают в себя:
- Создание графиков и диаграмм, где необходимо показать связь между различными переменными или данными.
- Отображение последовательности выполнения задач или процессов, где каждая точка представляет отдельное действие.
- Изображение сетей или связей, таких как семейное древо или диаграмма организационной структуры.
- Визуализация зависимостей или взаимосвязей между объектами или идеями.
Метод использования соединительных линий позволяет сделать представление информации более понятным и наглядным, а также помогает организовать и структурировать данные.
Примеры соединения точек из разных плоскостей
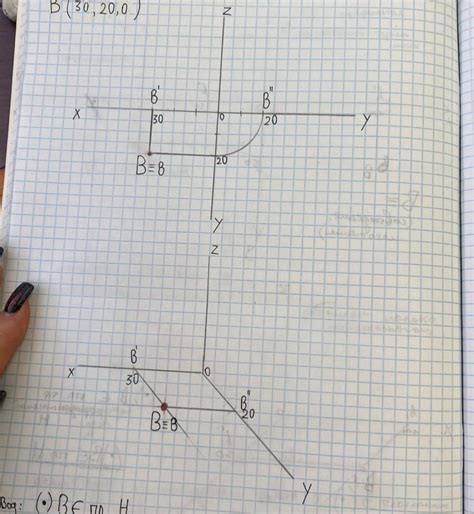
1. Соединение точек на фотографии и географической карте:
Этот метод соединения точек из разных плоскостей может быть полезен при создании туристических маршрутов или ориентировании на местности. Например, если у вас есть фотография достопримечательности, а также географическая карта района, вы можете использовать эти две плоскости для определения места расположения фотографии на карте.
Пример:
На фотографии изображен часовой механизм на старом здании. Чтобы определить место его расположения на географической карте, мы можем искать здание по сопоставляемым ориентирам, таким как окна или двери. Затем мы выделим точку на карте, которая соответствует примерному местоположению здания. Далее соединяем отмеченную точку на карте с точкой на фотографии. Таким образом, мы получаем визуальную связь между этими двумя плоскостями.
2. Соединение точек на архитектурных чертежах и трехмерной модели:
В архитектуре очень полезно иметь возможность соединять точки на чертежах с соответствующими элементами в трехмерной модели здания. Это помогает визуализировать отношение между плоскими чертежами и реальными объектами в пространстве.
Пример:
На чертеже здания отмечены расположение дверей. Чтобы визуализировать, как эти двери выглядят в реальности, можно создать трехмерную модель здания и соединить отмеченные точки на чертеже с соответствующими дверными элементами в модели. Это помогает архитекторам и клиентам лучше представить, как будут выглядеть различные элементы здания, основываясь на чертежах.
3. Соединение точек на астрономических снимках и стереоскопических изображениях:
Астрономы и научные исследователи часто используют метод соединения точек на астрономических снимках и стереоскопических изображениях для анализа разных плоскостей небесных объектов и формирования полного представления о их структуре и характеристиках.
Пример:
На астрономическом снимке видны различные звезды, планеты и галактики, которые могут находиться на разных расстояниях от Земли. Стереоскопические изображения позволяют получить трехмерное представление о небесных объектах. Метод соединения точек позволяет исследователям установить соответствие между определенной точкой на астрономическом снимке и точкой на стереоскопическом изображении. Такая техника может помочь в определении расстояний и формы небесных объектов.