Точки пересечения графиков функций - одна из важнейших концепций в математике и анализе. Они позволяют нам понять, когда и где две функции пересекаются друг с другом. Это может быть полезно для решения различных задач, моделирования явлений, построения графиков и многое другое.

Чтобы найти точки пересечения графиков функций, необходимо решить уравнение, которое задает эти функции. Для этого можно использовать различные методы, включая графический метод, метод подстановки, метод исключения и многое другое. Однако, самый распространенный и простой способ - это решить уравнение алгебраически.

Давайте рассмотрим пример:

Пусть у нас есть две функции: f(x) = x^2 - 4 и g(x) = 2x - 1. Необходимо найти точку пересечения этих функций.

Сначала заметим, что точки пересечения находятся там, где значения функций равны друг другу. То есть, нам нужно решить уравнение x^2 - 4 = 2x - 1. Решив это уравнение, мы найдем значение x, которое соответствует точке пересечения.

Как найти точки пересечения графиков функций

Для нахождения точек пересечения графиков функций можно использовать несколько подходов:

Метод графического представления: В этом методе необходимо построить графики функций на одной координатной плоскости и найти точки, в которых графики пересекаются. Этот метод позволяет получить наглядное представление о точках пересечения, однако он не является точным и может потребовать дополнительных итераций для получения более точных результатов.

Метод аналитического решения: В этом методе необходимо приравнять две функции друг к другу и решить полученное уравнение относительно аргумента. Найденные значения аргумента будут являться точками пересечения. Этот метод обеспечивает точные значения, но может потребовать сложных математических действий для решения уравнения.

Независимо от выбранного метода, для нахождения точек пересечения графиков функций необходимо иметь математическую модель этих функций. Эта модель может быть выражена аналитически или задана в виде таблицы значений.

Важно помнить, что графики функций могут иметь разное число точек пересечения - от нуля до бесконечности. Также возможно наличие точек пересечения между частями одного и того же графика.

Поиск точек пересечения графиков функций является важным инструментом анализа и решения задач в различных областях, таких как физика, экономика, инженерия и другие.

Полезные советы по поиску точек пересечения графиков функций

1. Метод подстановки

Один из самых простых способов найти точки пересечения графиков функций - это использование метода подстановки. Для этого необходимо приравнять две функции друг к другу и решить полученное уравнение. Например, если у нас есть две функции: f(x) = x^2 и g(x) = 2x - 1, мы можем приравнять их: x^2 = 2x - 1 и решить это уравнение для определения значения x. После этого, подставляем найденное значение x обратно в одну из функций, чтобы найти соответствующее значение y.

2. Использование графических калькуляторов

Если вам нужно найти точки пересечения графиков более сложных функций, вы можете воспользоваться графическими калькуляторами. Это программы или онлайн-инструменты, которые могут построить график функций и найти их точки пересечения автоматически. Просто введите функции в калькулятор и получите результаты.

3. Метод численного решения

Метод численного решения - это альтернативный подход к поиску точек пересечения графиков функций. Он основан на численных методах исчисления и позволяет найти приближенные значения точек пересечения. Для этого вам понадобятся математические программы или языки программирования, такие как Python или MATLAB, чтобы реализовать алгоритм численного решения.

Не зависимо от метода, который вы выбрали для поиска точек пересечения графиков функций, важно помнить, что эти точки представляют собой значения x и y, при которых функции равны друг другу. Они могут быть полезными при решении различных задач, от определения пересечений движущихся объектов до нахождения корней уравнений. Используйте эти советы, чтобы упростить процесс нахождения точек пересечения и улучшить вашу работу с графиками функций.

Примеры нахождения точек пересечения графиков функций

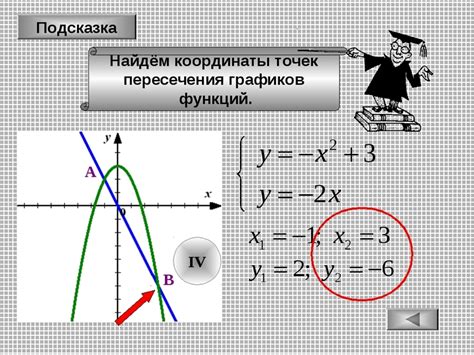
Пример 1:

Рассмотрим две функции:

Функция 1: y = x^2

Функция 2: y = 2x + 1

Для нахождения точки пересечения графиков этих функций, необходимо приравнять их:

x^2 = 2x + 1

x^2 - 2x - 1 = 0

Далее можно воспользоваться различными методами решения квадратного уравнения, например, формулой дискриминанта или методом завершения квадрата.

Решив уравнение, найдем значения x:

x1 = -0.4142 (приближенное значение)

x2 = 2.4142 (приближенное значение)

Подставив значения x в любую из функций, мы найдем точки пересечения:

Точка 1: (-0.4142, 0.1716)

Точка 2: (2.4142, 5.8284)

Пример 2:

Рассмотрим две функции:

Функция 1: y = sin(x)

Функция 2: y = cos(x)

Для нахождения точек пересечения графиков этих функций, необходимо приравнять их:

sin(x) = cos(x)

Так как sin(x) / cos(x) = tan(x), то уравнение можно записать как:

tan(x) = 1

Изучив график тангенса, мы можем заметить, что значения x, при которых tan(x) равен 1, находятся приблизительно в следующих точках: x = -0.7854, x = 2.3562, x = 5.4978 и т.д.

Подставив значения x в любую из функций, мы найдем точки пересечения:

Точка 1: (-0.7854, 0.7071)

Точка 2: (2.3562, 0.7071)

Точка 3: (5.4978, 0.7071)

Пример 3:

Рассмотрим две функции:

Функция 1: y = x

Функция 2: y = x^2

Для нахождения точек пересечения графиков этих функций, необходимо приравнять их:

x = x^2

x^2 - x = 0

Факторизуем уравнение:

x(x - 1) = 0

Таким образом, мы получаем две точки пересечения:

Точка 1: (0, 0)

Точка 2: (1, 1)