Трапеция - это геометрическая фигура, которая имеет две параллельные стороны, называемые основаниями, и две непараллельных стороны, называемые боковыми. В классификации трапеций выделяют трапеции прямоугольные, равнобедренные, равносторонние и другие. Однако, существует еще один особый вид трапеции - трапеция с центром симметрии.
Трапеция с центром симметрии - это трапеция, которая может быть симметрично развернута относительно своего центра на 180 градусов. Это означает, что при повороте трапеции на 180 градусов вокруг ее центра, она сохраняет свою форму и все свойства: параллельные стороны, углы и длины сторон.
Образующие трапеции с центром симметрии - это особые прямые, которые проходят через центр симметрии и делят трапецию на две равные части. То есть, если провести любую из образующих, она разделит трапецию на две равные по площади фигуры. Важно отметить, что образующие также являются диагоналями трапеции, которые соединяют противоположные вершины.
Определение трапеции с центром симметрии
Основным свойством трапеции с центром симметрии является то, что диагонали этой трапеции пересекаются в ее центре симметрии и делятся пополам. Другими словами, средняя линия трапеции, которая объединяет середины двух оснований, является диаметром окружности, вписанной в трапецию.
Также следует отметить, что трапеция с центром симметрии обладает свойством, что сумма противоположных углов равна 180 градусам. Это означает, что сумма угла между одной стороной и основанием и угла между противоположной стороной и основанием равна 180 градусам.
Для лучшего понимания свойств и образующих трапеции с центром симметрии рекомендуется рассмотреть примеры и изучить таблицы с данными, чтобы лучше вникнуть в особенности данной фигуры и легче работать с ней в математических расчетах и построениях.
| Свойства | Образующие |
|---|---|
| Центр симметрии | Диагонали пересекаются и делятся пополам |
| Сумма противоположных углов | 180 градусов |
Что такое трапеция с центром симметрии и как ее определить
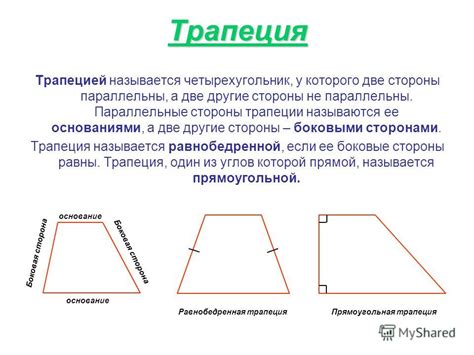
Определить, является ли данная фигура трапецией с центром симметрии, можно по следующим критериям:
- У фигуры должны быть две параллельные стороны - основания трапеции.
- Другие две стороны трапеции должны быть непараллельными.
- Диагонали трапеции должны пересекаться и образовывать перпендикуляр.
- Ось симметрии фигуры должна проходить через точку пересечения диагоналей - центр симметрии.
Трапеция с центром симметрии имеет ряд особенностей:
- Длины боковых сторон равны.
- Углы при основаниях равны.
- Сумма углов вокруг центра равна 360 градусов.
Трапеция с центром симметрии является частным случаем трапеции и имеет свои уникальные свойства и связи с другими геометрическими фигурами.
Свойства трапеции с центром симметрии
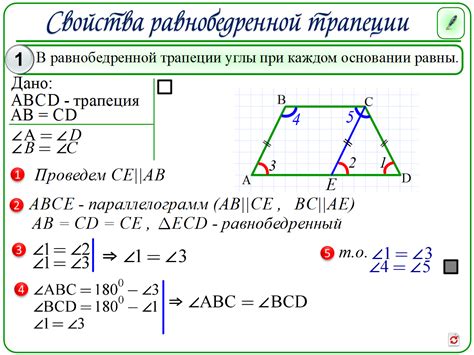
Главное свойство трапеции с центром симметрии заключается в том, что ее диагонали равны. Данное свойство следует из симметрии фигуры и геометрических свойств трапеции. При наличии оси симметрии, отражение одной части трапеции относительно оси приводит к получению другой половины, а значит, диагонали будут равны.
Также стоит отметить, что сумма углов при основании трапеции всегда равна 180 градусам, а две дополнительные углы (так называемые смежные углы) сумма которых также равна 180 градусам. Это свойство также относится к трапеции с центром симметрии.
Углы трапеции с центром симметрии и их свойства
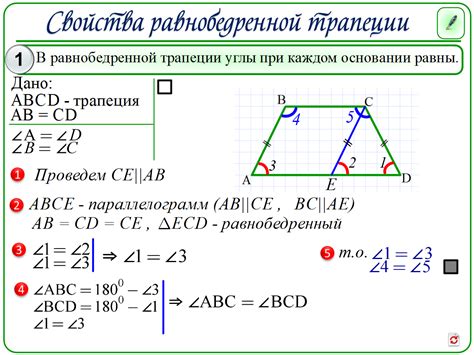
У трапеции с центром симметрии есть несколько интересных свойств, связанных с ее углами.
1. Противоположные углы в трапеции с центром симметрии равны между собой. Это означает, что угол, образованный более длинной стороной и одной из параллельных сторон, равен его противоположному углу, образованному более короткой стороной и другой параллельной стороной.
2. Сумма углов в трапеции с центром симметрии равна 360 градусов. В случае, если углы при основаниях трапеции равны, то каждый угол трапеции равен 90 градусам.
3. Пары углов, лежащих на одной и той же стороне относительно центра симметрии трапеции, в сумме также равны 180 градусам. Например, углы, лежащие на одной из параллельных сторон по разные стороны от центра, в сумме равны 180 градусам.
Важно: при рассмотрении углов трапеции с центром симметрии необходимо учитывать, что эти свойства выполняются только для трапеций, у которых есть центр симметрии. Для обычных трапеций эти свойства могут не соблюдаться.
Диагонали трапеции с центром симметрии и их связь с углами
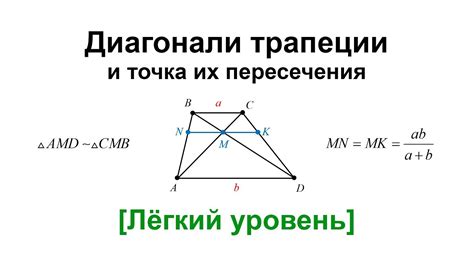
Диагонали трапеции играют важную роль в определении ее свойств и характеристик. Особое внимание следует обратить на трапеции с центром симметрии, у которых диагонали играют особую роль.
Всякую наименьшую диагональ, проведенную между двумя непараллельными сторонами трапеции, называют перпендикуляром. Его основные свойства:
- Перпендикуляр равен полусумме оснований трапеции.
- Углы между перпендикуляром и непараллельными сторонами трапеции суммируются до 180 градусов (определяются при равенстве диагоналей).
- Перпендикуляр делит нижнюю основу трапеции на две равные части.
Соответственно, диагональ, проведенная через середину нижней основы трапеции и соединяющая середины противоположных сторон, называется осью симметрии. У трапеции с центром симметрии ось симметрии является диагональю и проходит через ее центр.
Симметричные свойства боковых сторон трапеции
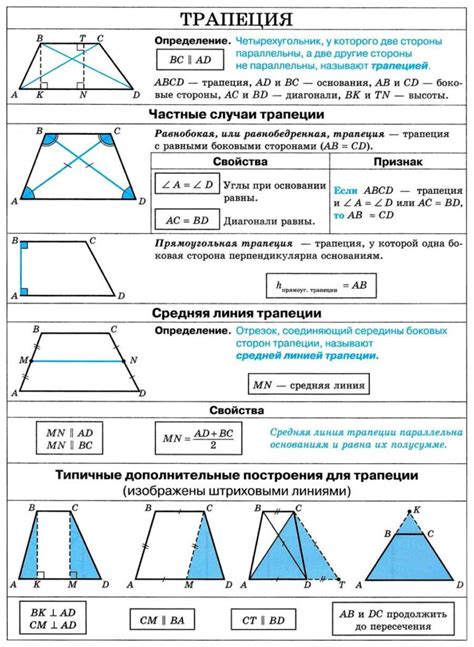
У трапеции с центром симметрии имеются интересные свойства, касающиеся ее боковых сторон.
1. Симметрия относительно вертикальной оси.
Боковые стороны трапеции являются симметричными относительно вертикальной оси проходящей через ее вершины. Это значит, что если мы рассмотрим два отрезка, образованных боковыми сторонами трапеции, то каждая точка одного отрезка будет соответствовать точке другого отрезка, отраженной относительно этой оси.
Пример:
Пусть боковые стороны трапеции равны AB и CD. Тогда для любой точки P на стороне AB найдется точка P', такая что P' будет симметрична относительно вертикальной оси проходящей через вершину трапеции.
2. Симметрия относительно горизонтальной оси.
Боковые стороны трапеции также являются симметричными относительно горизонтальной оси проходящей через середину отрезка между их точками пересечения с основаниями. Это означает, что каждая точка на одной стороне трапеции будет иметь симметричную относительно этой оси точку на другой стороне.
Пример:
Пусть боковые стороны трапеции равны AB и CD, а точки E и F являются точками их пересечения с основаниями трапеции. Тогда для любой точки Q на стороне AB найдется точка Q', такая что Q' будет симметрична относительно горизонтальной оси, проходящей через середину отрезка EF.
Формулы для вычисления параметров трапеции с центром симметрии

1. Периметр трапеции
Периметр трапеции с центром симметрии вычисляется по следующей формуле:
P = a + b + c + d,
где a и b – длины оснований, а c и d – длины боковых сторон. Если данные о длинах оснований и боковых сторон известны, то периметр можно легко подсчитать.
2. Площадь трапеции
Площадь трапеции с центром симметрии можно вычислить по формуле:
S = (a + b)h/2,
где a и b – длины оснований, а h – высота трапеции. Высоту можно найти, зная расстояние между основаниями или зная длины оснований и длину средней линии.
3. Диагональ трапеции
Диагональ трапеции с центром симметрии можно найти с помощью формулы:
d = √((a - b)² + 4h²)/2,
где a и b – длины оснований, а h – высота трапеции. Диагональ трапеции – это отрезок, соединяющий вершины, не принадлежащие одной стороне.
4. Углы трапеции
В трапеции с центром симметрии существуют два вида углов: острые углы и тупые углы. Острые углы образуются основаниями и боковыми сторонами, а тупые углы являются вертикальными противолежащими углами.
Используя эти формулы, вы сможете вычислить основные параметры трапеции с центром симметрии и проводить различные геометрические вычисления связанные с этой фигурой.
Формула для вычисления площади трапеции с центром симметрии

Пусть основания трапеции равны a и b, а высота равна h. Тогда формула для вычисления площади трапеции с центром симметрии имеет вид:
S = [(a + b) * h] / 2
Где S - площадь трапеции, a и b - длины оснований, h - высота.
Используя эту формулу, вы сможете легко вычислить площадь трапеции с центром симметрии, зная длины оснований и высоту фигуры.
Формула для вычисления периметра трапеции с центром симметрии

Периметр трапеции с центром симметрии вычисляется путем сложения длин всех сторон трапеции.
Пусть a и b - длины оснований трапеции, c - длина боковой стороны, а d - длина средней линии (высоты).
Тогда периметр трапеции с центром симметрии можно вычислить по следующей формуле:
| Периметр | = | a + b + 2c |
|---|
В данной формуле длины оснований (a и b) складываются с удвоенной длиной боковой стороны (c), поскольку у трапеции с центром симметрии боковые стороны равны. Полученная сумма является периметром трапеции.