Треугольник Гиббса-Розенбаума получил свое название в честь английского философа Гуга Гиббса и российского математика Владимира Розенбаума. Этот треугольник является особенным в математике и часто используется в геометрическом анализе и теории вероятностей. Его построение может быть достаточно сложным заданием, но существуют различные методы, которые позволяют получить треугольник Гиббса-Розенбаума с высокой точностью.

Один из методов строительства треугольника Гиббса-Розенбаума основан на использовании векторов. Для начала, выбираются три точки на плоскости, которые являются вершинами треугольника. Затем, для каждой вершины треугольника вычисляются ее векторные координаты. Зная векторные координаты трех вершин треугольника, можно построить соответствующий треугольник Гиббса-Розенбаума.

Другой способ построения треугольника Гиббса-Розенбаума основан на понятии матриц. Для этого необходимо задать матрицу, содержащую векторные координаты трех вершин треугольника. Затем, с помощью матричных операций, можно получить треугольник Гиббса-Розенбаума. Этот метод является более сложным, но обладает более высокой точностью, особенно при работе с большим количеством вершин треугольника.

Способы построения треугольника Гиббса-Розенбаума имеют широкое применение в различных областях науки и техники, таких как компьютерная графика, моделирование, анализ данных и других. Они позволяют получить треугольник, которым можно удобно оперировать и проводить различные вычисления. Знание этих методов позволяет решать сложные задачи и получать более точные результаты в научных исследованиях и прикладных работах.

Что такое треугольник Гиббса-Розенбаума и как его построить?

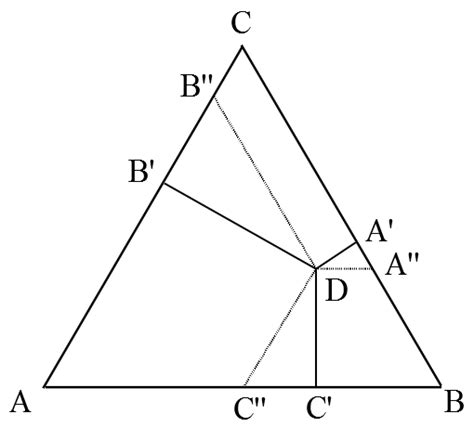
Данный треугольник назван в честь ученых Гиббса и Розенбаума, которые впервые предложили метод его построения в 2010 году.

Построение треугольника Гиббса-Розенбаума осуществляется следующим образом:

1. Найдите середины сторон произвольного треугольника.
2. Проведите от середины каждой стороны линию, параллельную противоположной стороне.
3. Проведите от точки пересечения каждой пары параллельных линий линии, ведущие к противоположным углам треугольника.
4. Проведите от каждого угла треугольника линию, проходящую через точку пересечения противоположных параллельных линий.
5. Треугольник Гиббса-Розенбаума будет состоять из трех маленьких треугольников, образованных линиями, проведенными в предыдущем шаге.

Стоит отметить, что треугольник Гиббса-Розенбаума обладает некоторыми интересными свойствами, которые могут быть использованы в математике и геометрии.

Треугольник Гиббса-Розенбаума является примером простой и элегантной геометрической фигуры, которая может быть использована для различных задач и исследований.

История и описание треугольника Гиббса-Розенбаума

Создание треугольника Гиббса-Розенбаума было вдохновлено исследованиями в области комбинаторики и численных последовательностей. Треугольник был впервые опубликован в статье Гиббса и Розенбаума в 1972 году. Они представили новый способ генерации числового треугольника, который имеет несколько уникальных свойств и структуру.

Треугольник Гиббса-Розенбаума имеет следующие особенности:

• Первая строка треугольника состоит только из единиц.
• Каждый элемент треугольника равен сумме двух элементов, расположенных над ним в предыдущей строке.
• При этом, второй элемент каждой строки равен сумме всех элементов предыдущей строки, и так далее.
• Элементы треугольника Гиббса-Розенбаума также связаны с биномиальными коэффициентами и комбинаторными аспектами.

Треугольник Гиббса-Розенбаума можно представить в виде таблицы или графического изображения, позволяющего легко визуализировать его структуру и числовые значения. Этот треугольник находит применение в различных областях математики и информатики, включая теорию чисел, комбинаторику, вероятность, алгоритмы и т.д.

Способ 1: Построение треугольника Гиббса-Розенбаума с использованием транспортира

Для построения треугольника Гиббса-Розенбаума с использованием транспортира следуйте следующим шагам:

1. На листе бумаги поставьте точку A – центр внешней окружности, и проведите через нее два перпендикуляра – ось OX и ось OY.

2. На оси OY отметьте точку B – центр внутренней окружности.

3. Возьмите транспортир и приложите его к оси OX таким образом, чтобы 0 градусов было направлено вправо.

4. Найдите угол, равный 30 градусам, и откладывайте его от оси OY, начиная с точки B.

5. Поставьте точку C на пересечении откладываемой линии и внешней окружности.

6. Проведите отрезки AB, BC и AC – это будут стороны треугольника Гиббса-Розенбаума.

Таким образом, вы построили треугольник Гиббса-Розенбаума с использованием транспортира.

Способ 2: Построение треугольника Гиббса-Розенбаума с использованием рулетки

1. Отметьте на плоскости начальную точку, которую обозначим как точку А.
2. Возьмите рулетку и измерьте от точки А отрезок, который будет первой стороной треугольника. Поставьте метку и обозначьте конечную точку как точку В.
3. Поместите точку А рядом с точкой В и повторите шаг 2, чтобы получить вторую сторону треугольника. Обозначьте конечную точку меткой и назовите ее точкой С.
4. Раскройте рулетку отметкой точки А и измерьте отрезок, равный первой стороне треугольника. Поставьте метку и обозначьте конечную точку как точку D.
5. Измерьте отрезок от точки D, равный второй стороне треугольника, и обозначьте конечную точку меткой. Эта точка будет точкой E.

Таким образом, вы получите треугольник Гиббса-Розенбаума, у которого стороны AB и BC представляют собой равные отрезки, а угол ABC равен 90 градусов.

Способ 3: Построение треугольника Гиббса-Розенбаума с использованием циркуля

Для начала построим окружность с центром в точке B и радиусом AB. Затем, используя циркуль, проведем дугу окружности радиусом BC с центром в точке C. Пусть точка D - точка пересечения дуги и прямой AC.

Теперь используя определение треугольника Гиббса-Розенбаума, можно провести прямую BE, которая проходит через точку D и перпендикулярна прямой AC. Проведем также прямую DF, которая также проходит через точку D и перпендикулярна прямой AB.

И вот, треугольник Гиббса-Розенбаума ABC готов! Он представляет собой треугольник, у которого все три стороны представляют собой хорды окружности с центром в точке B, а точки E и F являются серединами этих хорд.