Треугольник – один из наиболее изучаемых и узнаваемых геометрических объектов. Многие уже с детства знают его форму: три стороны и три угла, которые собираются вместе, образуя эту замечательную фигуру. Однако, несмотря на свою простоту, треугольник может вызывать некоторые вопросы и дискуссии. Одним из основных споров, касающихся треугольника, является: это всего лишь линия из трех звеньев или у него есть что-то большее, сокрытое в своей структуре?
Для понимания этого вопроса необходимо обратиться к основам геометрии. Треугольник – это не просто три соединенных линии или звена, как могло бы показаться на первый взгляд. Он – это геометрическая фигура, обладающая определенными свойствами и характеристиками. Если взглянуть на треугольник, заметны его три стороны и три угла.
Со стороны структуры треугольника, его можно рассматривать как линию из трех звеньев. Но это лишь один из аспектов, которые следует учитывать. Треугольник имеет уникальные свойства, к которым относятся: сумма углов треугольника равна 180 градусам, сумма длин двух сторон треугольника всегда больше, чем длина третьей стороны, и так далее. Все эти характеристики делают треугольник особой фигурой, а не просто линией из трех звеньев.
Треугольник - линия из трех звеньев или нет?

Основное условие для существования треугольника заключается в том, что сумма длин двух его сторон должна быть больше, чем длина третьей стороны. Если это условие не выполняется, то треугольник не может существовать.
Также существуют специальные типы треугольников, которые имеют дополнительные характеристики. Например, равносторонний треугольник имеет все три стороны и все три угла равными между собой. Равнобедренный треугольник имеет две равные стороны и два равных угла. Прямоугольный треугольник имеет один прямой угол, равный 90 градусов.
Треугольники являются основными фигурами в геометрии и широко используются в различных областях, таких как архитектура, инженерное дело, графика и многих других.
Определение треугольника в геометрии
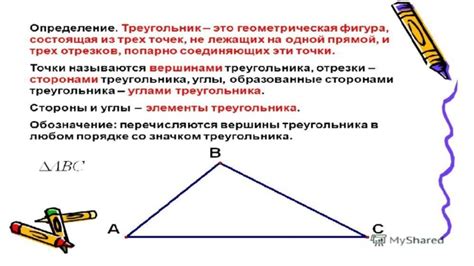
Для определения треугольника в геометрии необходимо выполнение следующих условий:
- У треугольника должно быть ровно три стороны.
- Сумма длин любых двух сторон треугольника должна быть больше длины третьей стороны. Это неравенство называется неравенством треугольника.
Также треугольники можно классифицировать по различным свойствам:
- По длинам сторон - равносторонний (все стороны равны), равнобедренный (две стороны равны), разносторонний (все стороны разные).
- По величине углов - прямоугольный (один угол равен 90 градусов), остроугольный (все углы меньше 90 градусов), тупоугольный (один угол больше 90 градусов).
- По положению в плоскости - прямолинейный (вершины лежат на одной прямой), непрямолинейный (вершины не лежат на одной прямой).
Изучение треугольников и их свойств в геометрии позволяет решать различные задачи, например, находить площадь треугольника, находить высоту и медианы треугольника, а также определять его подобие и конгруэнтность.
Основные характеристики треугольника

Основные характеристики треугольника:
Стороны: Треугольник имеет три стороны, обозначаемые обычно буквами a, b и c. Длина каждой стороны может быть разной.
Углы: В треугольнике существуют три угла, обозначаемые обычно как α (альфа), β (бета) и γ (гамма). Сумма углов треугольника всегда равна 180 градусов.
Периметр: Периметр треугольника - это сумма длин всех его сторон. Обозначается символом P.
Площадь: Площадь треугольника - это мера его поверхности. Вычисляется по формуле S = 0,5 * a * h, где a - одна из сторон треугольника, h - высота, опущенная на эту сторону.
Высоты: Высота треугольника - это отрезок, опущенный из вершины треугольника до прямой, содержащей противоположную сторону. Треугольник имеет три высоты, каждая из которых считается отдельно.
Медианы: Медианы треугольника - это отрезки, соединяющие вершину треугольника с серединой противоположной стороны. Треугольник имеет три медианы.
Биссектрисы: Биссектрисы треугольника - это прямые, разделяющие угол пополам. Треугольник имеет три биссектрисы.
Знание основных характеристик треугольника является важным для решения задач по геометрии и позволяет более глубоко понять его структуру и свойства.
Существование треугольника согласно геометрическим правилам
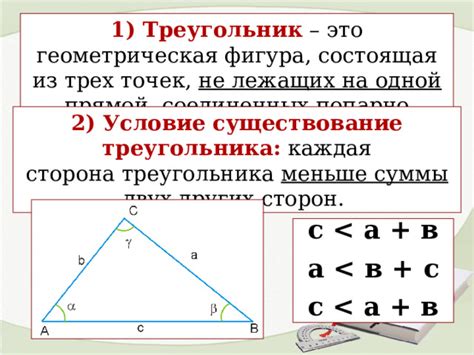
Существует несколько правил, которые помогают определить, можно ли построить треугольник с заданными длинами сторон:
1. Неравенство треугольника:
Сумма любых двух сторон треугольника всегда должна быть больше третьей стороны. Иначе треугольник не может существовать. Математически это выражается следующим образом: a + b > c, где a, b и c – длины сторон треугольника.
2. Угловое условие:
Сумма углов треугольника всегда равна 180 градусам. Если у нас есть три значения углов, сумма которых не равна 180 градусам, значит, треугольник с такими углами не может существовать.
3. Метод построения треугольника:
Если заданы длины сторон треугольника, то его можно построить с помощью метода построения, например, с помощью нитей и линейки. Если в процессе построения трех сторон образуется фигура с тремя углами, которые сходятся в одной точке, тогда треугольник с такими сторонами существует.
Важно помнить, что соблюдение этих правил не гарантирует принадлежность треугольника определенному типу (остроугольный, тупоугольный или прямоугольный), а только позволяет определить, возможно ли его построение.
Разновидности треугольников по длинам сторон и углам
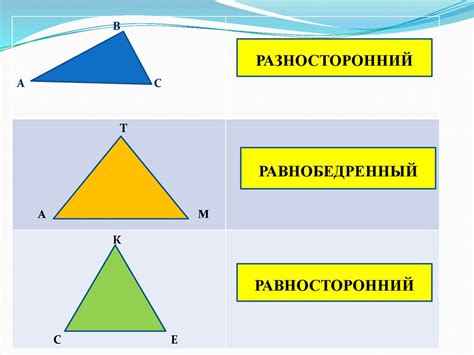
Треугольники могут классифицироваться по различным критериям, включая длины сторон и значения углов. В данном разделе мы рассмотрим разновидности треугольников по этим параметрам.
По длинам сторон:
- Равносторонний треугольник - треугольник, у которого все стороны имеют одинаковую длину.
- Равнобедренный треугольник - треугольник, у которого две стороны имеют одинаковую длину.
- Разносторонний треугольник - треугольник, у которого все стороны имеют разные длины.
По значениям углов:
- Остроугольный треугольник - треугольник, у которого все углы острые (меньше 90°).
- Прямоугольный треугольник - треугольник, у которого один из углов равен 90°.
- Тупоугольный треугольник - треугольник, у которого один из углов больше 90°.
Треугольники могут также сочетать различные характеристики по длинам сторон и углам. Например, равнобедренный треугольник может быть остроугольным или тупоугольным.
Понимание разных разновидностей треугольников помогает в изучении их свойств и в решении задач, связанных с геометрией.
Формула Пифагора и ее применение в треугольнике
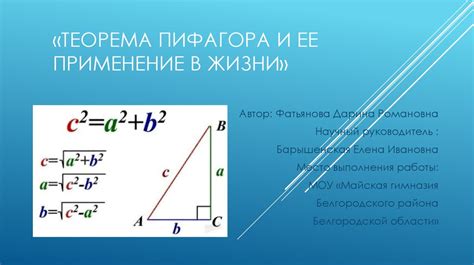
Формула Пифагора утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Гипотенуза - это сторона треугольника, которая лежит напротив прямого угла.
Формализованная формула Пифагора для треугольника со сторонами a, b и c можно записать следующим образом:
| c² = a² + b² |
Эта формула может быть использована для нахождения длины одной из сторон треугольника, если известны длины двух других сторон. Также она позволяет проверить, является ли треугольник прямоугольным.
Например, если длины двух катетов треугольника равны 3 и 4, то можно использовать формулу Пифагора, чтобы найти длину гипотенузы:
| a = 3 | b = 4 |
| a² = 9 | b² = 16 |
| a² + b² = 25 | c² = 25 |
| c = √25 = 5 | |
Таким образом, длина гипотенузы треугольника с катетами 3 и 4 равна 5. Этот треугольник является прямоугольным треугольником, так как выполнена формула Пифагора.
Формулу Пифагора можно также использовать для проверки, является ли треугольник прямоугольным или нет. Если выполнена формула Пифагора для трех сторон треугольника, то треугольник является прямоугольным.
Важно отметить, что формула Пифагора применима только в прямоугольных треугольниках. Для остроугольного и тупоугольного треугольников эта формула не применима.
Теоремы о сумме углов треугольника
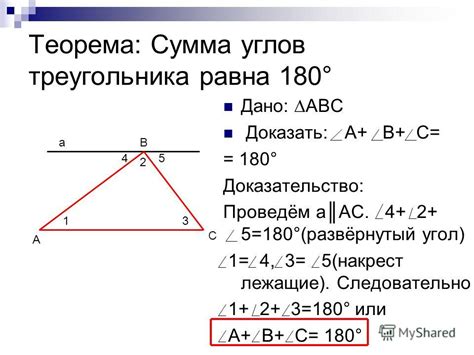
Сумма углов в треугольнике всегда равна 180 градусов. Это основополагающая теорема геометрии, которая имеет несколько следствий.
Внутренние углы треугольника: сумма внутренних углов треугольника всегда равна 180 градусам. Это означает, что если известны два угла треугольника, можно легко вычислить третий угол.
Углы при основании: углы, образованные боковыми сторонами треугольника и основанием, всегда суммируются до 180 градусов. Это следует из свойства, что сумма углов треугольника равна 180 градусам.
Углы между сторонами и диагоналями: углы, образованные сторонами и диагоналями треугольника, также всегда суммируются до 180 градусов.
Выведенные теоремы о сумме углов треугольника важны для изучения и понимания основ геометрии. Они помогают решать различные геометрические задачи и строить различные фигуры.
Построение треугольника с помощью геометрических инструментов
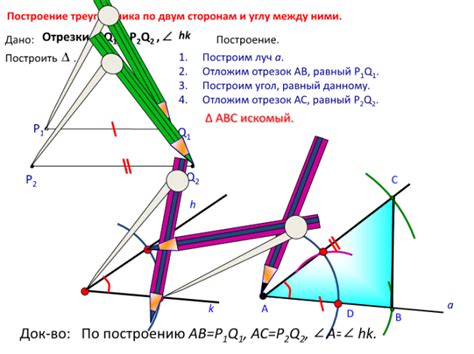
Для построения треугольника с помощью геометрических инструментов необходимо знать его стороны или углы. Существует несколько способов это сделать:
1. Построение по сторонам:
Для того чтобы построить треугольник по сторонам, необходимо использовать циркуль и линейку. Сначала выбирают одну из сторон треугольника и отмечают ее на линейке. Затем с помощью циркуля откладывают эту длину на линейке от начальной точки и ставят точку. Аналогично поступают с другими сторонами треугольника. После того как все три точки отмечены, соединяют их линиями. Полученную фигуру можно назвать треугольником.
2. Построение по углам:
Для построения треугольника по углам потребуется угломер и линейка. Сначала выбирают один из углов треугольника и откладывают его в угломере. Затем на линейку откладывают отмеченный угол и ставят точку. Аналогично поступают с другими углами треугольника. После того как три точки отмечены, соединяют их линиями. Таким образом получается треугольник.
3. Построение по стороне и углу:
Если известна одна сторона треугольника и прилежащий к ней угол, можно построить треугольник, используя циркуль и угломер. Для этого выбирают на линейке длину известной стороны и отмечают точку. Затем с помощью угломера откладывают известный угол от этой точки и ставят еще одну точку на линейке. После этого, с помощью циркуля, отмечают радиус от новой точки до первой и ставят окружность. После пересечения окружности и линии, соединяют полученные точки и получают треугольник.
Важно помнить, что для корректного построения треугольника необходимо выбирать и откладывать значения с учетом их взаимного расположения и свойств треугольника.
Практическое применение треугольников в различных областях

1. Строительство: Треугольники используются в строительстве для определения углов зданий, расчета длины сторон и поверхности, а также для создания устойчивых и прочных конструкций. Они помогают архитекторам и инженерам создавать эффективные и безопасные здания.
2. Навигация: В морской навигации треугольники используются для определения местоположения судна и построения маршрута. Например, с помощью геодезического треугольника можно определить географические координаты местности.
3. Авиация: Треугольники применяются в авиации при разработке крыла самолетов и расчете аэродинамических характеристик. Знание треугольников помогает инженерам создавать легкие и прочные конструкции, а также повышать безопасность полетов.
4. Геодезия: В геодезии треугольники используются для измерения и построения карт. Также с их помощью определяются высоты и расстояния на местности, что необходимо при планировании строительных проектов и землеустройстве.
5. Компьютерная графика: Треугольники широко применяются в компьютерной графике для построения трехмерных моделей и создания реалистичных визуализаций. Они являются основными элементами трехмерной графики и позволяют программным средствам создавать сложные эффекты и анимацию.
6. Медицина: Треугольники применяются в медицине для анализа формы и размеров органов, планирования операций и изготовления протезов. Например, в стоматологии с помощью треугольников определяют форму зубов и создают индивидуальные протезы.
Треугольники - универсальные фигуры, которые находят широкое применение в различных областях и играют важную роль в практической жизни и научных исследованиях.