Линейные функции являются одним из фундаментальных понятий математики. Они представляют собой простейший тип функций, графики которых являются прямыми линиями на плоскости. Одним из важных свойств линейных функций является нахождение их вершин – точек, в которых график функции достигает своего экстремума.
Существует несколько способов нахождения вершин линейной функции. Первый способ – это аналитический метод. Для этого необходимо записать уравнение линейной функции в общем виде y = kx + b, где k – коэффициент пропорциональности, а b – свободный член. Получив уравнение, можно легко определить координаты вершины. Вершина функции есть точка экстремума графика, при которой происходит смена направления роста или убывания функции. При этом, если коэффициент k положителен, то график функции будет направлен вправо, а если отрицательный – влево.
Второй способ нахождения вершин линейной функции – это графический метод. Для этого необходимо построить график функции и определить экстремум. Для линейной функции это будет являться точка, в которой прямая меняет свое направление роста или убывания. Найдя эту точку, можно определить ее координаты – это и будут координаты вершины функции.
Третий способ нахождения вершин линейной функции – это геометрический метод. Для применения этого метода необходимо знать основные геометрические понятия, такие как параллельность и перпендикулярность прямых. Используя эти знания, можно определить между какими прямыми линиями находится вершина функции и легко найти ее координаты.
Способы нахождения вершин линейной функции
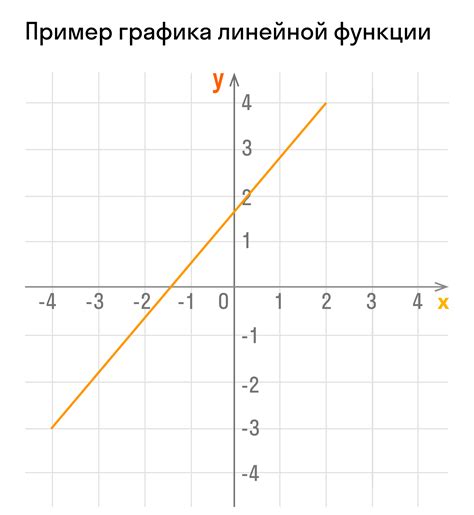
1. Геометрический метод. Для нахождения вершины линейной функции нужно построить график данной функции на координатной плоскости. Затем определить точку, в которой функция достигает своего максимума или минимума. Эта точка будет являться вершиной функции.
2. Алгебраический метод. Линейная функция обычно записывается в виде уравнения y = kx + b, где k - коэффициент наклона прямой, а b - свободный член. Вершина линейной функции находится в точке с координатами x = -b/2k и y = f(x), где f(x) - значение функции в этой точке.
3. Использование производной. Если данная линейная функция задана в виде y = mx + c, то вершина функции находится в точке с абсциссой x = -c/m и ординатой y = f(x), где f(x) - значение функции в этой точке. Этот метод основан на свойствах производной функции и может быть применен только к линейным функциям.
Важно помнить, что вершина линейной функции может быть как максимальной, так и минимальной, в зависимости от коэффициента наклона прямой. Эти способы нахождения вершин линейной функции являются универсальными и могут быть использованы для любой линейной функции.
Метод графического представления

Для построения графика линейной функции необходимо знать две точки. Первая точка задается координатами (x1, y1), а вторая точка - координатами (x2, y2). Для нахождения вершин линейной функции можно использовать три различных способа:
1. Нахождение вершины функции по формуле. Для этого используется формула x = -b/2a, где a и b - коэффициенты линейной функции. Подставляем найденное значение x в уравнение и находим значение y. Таким образом, получаем координаты вершины функции (x, y).
2. Прямой и перпендикулярной линии. Для этого проводим прямую линию, параллельную заданной линейной функции. Затем проводим перпендикулярную линию к данной прямой с началом в середине отрезка между двумя точками, заданными уравнением линейной функции. Пересечение перпендикулярной и прямой линий даст нам координаты вершины функции.
3. Зеркальное отражение. Для этого проводим прямую линию через середину отрезка между двумя точками, заданными уравнением линейной функции. Строим прямую, перпендикулярную заданной линии и проводим ее через точку пересечения двух прямых. Координаты точки пересечения дадут нам координаты вершины функции.
Метод графического представления является наглядным и позволяет визуально определить координаты вершин линейной функции.
Метод квадратного трехчлена

Для начала необходимо записать линейную функцию в форме y = ax + b, где a и b - коэффициенты функции. Затем необходимо найти вершину графика функции, используя формулу x = -b / 2a.
Подставим найденное значение x в исходную функцию и получим значение y. В результате получим координаты вершины графика функции.
Применение метода квадратного трехчлена позволяет найти вершину графика линейной функции без необходимости построения графика или использования геометрических методов. Этот метод является более быстрым и удобным способом нахождения вершин линейных функций.
Метод дифференциального исчисления

Производная функции определяется как предел отношения изменения значения функции к изменению ее аргумента. В случае линейной функции производная постоянна и равна коэффициенту при переменной в функции.
Для нахождения точек экстремума линейной функции с помощью метода дифференциального исчисления необходимо приравнять производную к нулю и решить полученное уравнение относительно переменной. Полученные значения переменной будут являться координатами точек вершин функции.
Следует отметить, что метод дифференциального исчисления применим только для функций, у которых производная существует и непрерывна на интервале, на котором исследуется функция.
| Пример | Исходная функция | Производная | Точка экстремума |
|---|---|---|---|
| 1 | y = 3x + 2 | 3 | (0, 2) |
| 2 | y = -2x + 5 | -2 | (0, 5) |
В таблице приведены примеры линейных функций, их производные и точки экстремума. Из таблицы видно, что в обоих случаях производная функции равна коэффициенту при переменной в функции. Точки экстремума получаются при x = 0, что соответствует вертикальной прямой, проходящей через точку (0, y).
Сводная информация

Существуют три способа нахождения вершин линейной функции:
- Графический способ: построение графика функции и определение точки с наибольшим или наименьшим значением.
- Аналитический способ: использование формулы для нахождения вершины функции, которая зависит от коэффициентов a, b и c.
- Геометрический способ: нахождение вершины функции как точки пересечения прямых, прямая которых является касательной к графику функции.
Все эти способы позволяют определить координаты вершины линейной функции и более точно изучить свойства этой функции.
Необходимо выбрать наиболее удобный способ в зависимости от поставленной задачи и доступных данных о функции.