Графики функций являются важным инструментом в математике и науках, связанных с анализом данных. Построение графиков позволяет наглядно представить зависимость между переменными и визуально исследовать различные особенности функций. Одной из наиболее распространенных классификаций функций является дробно-линейная функция, которая представляет собой отношение двух линейных функций.

Дробно-линейная функция определяется следующим образом: y = (ax + b) / (cx + d), где a, b, c и d - это коэффициенты функции, а x и y - переменные.

Для построения графика дробно-линейной функции необходимо выполнить несколько шагов. Во-первых, необходимо определить область значений, на которой будет рассматриваться функция. Затем следует вычислить значения функции для различных значений переменной x в указанной области. Для этого можно выбрать несколько произвольных значений x и вычислить соответствующие значения y, используя заданную функцию. После этого можно построить график, отображая полученные точки на плоскости.

Определение дробно линейной функции

Данный вид функции представляет собой отношение двух линейных функций и характеризуется тем, что в знаменателе присутствует линейная функция от переменной x.

График дробно линейной функции может представлять собой прямую линию, гиперболу или их комбинацию в зависимости от значений коэффициентов a, b, c и d. При анализе графика необходимо обращать внимание на такие характеристики, как асимптоты, точки пересечения осей координат и области значений функции.

Раздел 1: Свойства дробно линейной функции

Дробно линейные функции могут иметь различные свойства, которые могут быть определены при анализе их графиков и алгебраических свойств.

Важным свойством дробно линейной функции является ее область определения. Область определения состоит из значений x, при которых функция является определенной и не имеет деления на ноль. Для дробно линейной функции допустимыми значениями x являются все числа, кроме решений уравнения cx + d = 0.

График дробно линейной функции может иметь различные формы, в зависимости от значений коэффициентов a, b, c и d. Начертание графика может быть выпуклым вниз или выпуклым вверх, в зависимости от того, является ли коэффициент c положительным или отрицательным.

График дробно линейной функции также может иметь вертикальные и горизонтальные асимптоты. Вертикальные асимптоты возникают тогда, когда знаменатель функции равен нулю, то есть при cx + d = 0. Горизонтальные асимптоты возникают, когда степени числителя и знаменателя одинаковы и отношение их коэффициентов равно некоторому числу.

Дробно линейные функции также подчиняются алгебраическим свойствам, таким как сложение, вычитание, умножение и деление. Они также могут быть преобразованы для получения простой линейной функции, путем сокращения коэффициентов или умножения на их общий множитель.

Изучение свойств дробно линейных функций может помочь в понимании их поведения и использовании их для решения различных задач в математике и физике.

Существование области определения

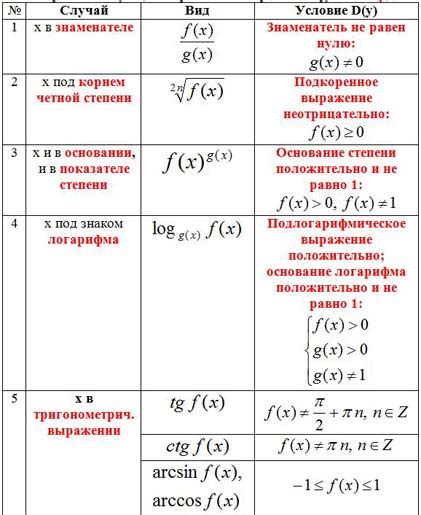
Для дробно-линейных функций область определения определяется ограничениями на аргументы, которые приводят к делению на ноль. Деление на ноль является недопустимой операцией в математике, поэтому необходимо исключить значения аргумента, при которых такое деление возможно.

Чтобы найти область определения дробно-линейной функции, необходимо решить уравнение, при котором знаменатель функции равен нулю:

знаменатель = 0

Решив это уравнение, можно найти значения аргумента, при которых функция не определена. Для этих значений аргумента на графике будет присутствовать вертикальная асимптота или разрыв функции.

Кроме того, область определения дробно-линейной функции может быть ограничена другими условиями, например, в случае, если функция содержит квадратный корень или логарифм, необходимо проверить, что выражение под корнем или в аргументе логарифма неотрицательно.

Таким образом, определение области определения является важным шагом при построении графика дробно-линейной функции, и позволяет избежать деления на ноль и других недопустимых операций.

Существование области значений

При построении графика дробно линейной функции необходимо учитывать существование области значений. Область значений функции определяет все возможные значения, которые функция может принимать. Для дробно линейной функции эту область нужно установить, чтобы график был корректным.

Для определения области значений дробно линейной функции необходимо учитывать два фактора:

1. Знаменатель функции

Знаменатель функции определяет значения, при которых функция может стать равной нулю. Например, если в знаменателе функции есть множитель (x - 2), то значение x = 2 приведет к делению на ноль, что противоречит математическим правилам. Поэтому значение x = 2 не может принадлежать области значений функции.

2. Числитель функции

Числитель функции определяет значения, которые функция может принимать. Например, если числитель функции имеет множитель (x + 1), то функция может принимать любые значения, кроме x = -1. Поэтому значение x = -1 также не может принадлежать области значений функции.

Таким образом, чтобы построить график дробно линейной функции, необходимо исключить из области значений все значения, которые противоречат математическим правилам. Это позволит получить корректное представление функции на графике.

Монотонность функции

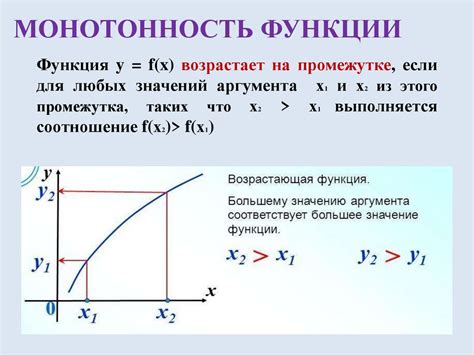
Функция называется монотонно возрастающей на интервале, если значение функции увеличивается при увеличении аргумента. То есть, если для любых двух точек на интервале, x₁ и x₂, таких что x₁

Функция называется монотонно убывающей на интервале, если значение функции уменьшается при увеличении аргумента. То есть, если для любых двух точек на интервале, x₁ и x₂, таких что x₁ f(x₂).

Функция называется обладающей переменной монотонностью на интервале, если она не является ни монотонно возрастающей, ни монотонно убывающей на этом интервале.

Для построения графика дробно-линейной функции необходимо определить ее монотонность на каждом интервале, на котором она определена. Это помогает представить график в виде упорядоченных участков, что позволяет лучше понять поведение функции и предсказать его приближенное изменение.

Асимптоты графика

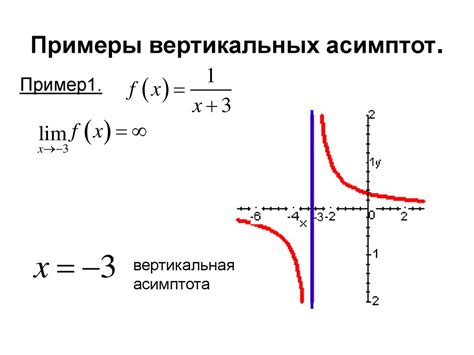
График дробно линейной функции может иметь две основные асимптоты: горизонтальную и вертикальную.

Горизонтальная асимптота определяет направление, в котором график стремится приближаться к постоянному значению по оси ординат. Она может быть найдена с помощью анализа предела функции при стремлении аргумента к бесконечности или минус бесконечности. Если этот предел существует и является конечным числом, то график имеет горизонтальную асимптоту, которая задается уравнением y = c, где c - значение предела.

Вертикальная асимптота определяет направление, в котором график функции стремится к бесконечности по оси ординат. Она может быть найдена с помощью анализа пределов функции при стремлении аргумента к конкретному значению. Если хотя бы одна из этих функций имеет предел, равный плюс или минус бесконечности, то график функции имеет в этой точке вертикальную асимптоту. Уравнение вертикальной асимптоты задается в виде x = a, где a - значение, к которому стремится аргумент функции.

Асимптоты графика дробно линейной функции отражают ее поведение на границе определения или в пределе. Знание и использование асимптот позволяет более точно изобразить и анализировать график такой функции.

Раздел 2: Построение графика дробно линейной функции

Чтобы построить график дробно линейной функции, мы должны следовать нескольким шагам:

1. Определить область определения функции. Область определения - это множество значений аргумента, при которых функция имеет смысл. Для дробно линейной функции область определения - это все действительные числа, кроме значений, при которых знаменатель равен нулю.
2. На основе области определения определить нули функции. Нулями функции являются те значения аргумента, при которых функция равна нулю. Чтобы найти нули функции, мы должны приравнять числитель функции к нулю и решить полученное уравнение.
3. Построить таблицу значений функции. Мы выбираем несколько значений аргумента из области определения и находим соответствующие значения функции, подставляя их в уравнение функции.
4. Используя полученные значения, строим график функции на координатной плоскости. Значения аргумента откладываем по горизонтальной оси (ось x), а значения функции откладываем по вертикальной оси (ось y).

Важно учитывать особенности дробно линейной функции, такие как вертикальные и горизонтальные асимптоты, экстремумы и поведение функции при различных значениях аргумента.

Используя эти шаги, мы можем построить график дробно линейной функции и лучше понять ее свойства и графическое представление.