Умножение матриц - одна из основных операций в линейной алгебре, которая находит широкое применение в различных областях, таких как физика, экономика и информатика. Однако многие сталкиваются с ограничением в размерах умножаемых матриц и думают, что умножение матриц разных размеров невозможно. В этой статье мы разъясним, что умножение матриц разных размеров действительно возможно и какие особенности с ним связаны.
Перед тем, как рассматривать случай умножения матриц разных размеров, важно вспомнить, что имеется в виду, когда говорят о умножении матриц. Умножение матриц - это процесс, при котором из двух матриц получается третья матрица, элементы которой являются комбинациями элементов исходных матриц, умноженных друг на друга и сложенных. Умножение матриц широко используется для решения систем уравнений, нахождения определителей и обратных матриц, а также для решения различных задач оптимизации.
Возможность умножения матриц разных размеров зависит от их конкретных размерностей и определённых правил. Считается, что умножение матриц возможно только в случае, когда число столбцов первой матрицы равно числу строк второй матрицы. Но что делать, если размерности матрицы не удовлетворяют этому условию? В таких случаях возникает несколько вариантов: умножение по правилу онтогнитна, умножение на матрицу-строку или на матрицу-столбец, а также умножение матриц на блоки. В каждом из этих вариантов есть свои особенности и ограничения, которые требуют дополнительного изучения и понимания.
Понятие умножения матриц

Умножение матриц является одной из основных операций в линейной алгебре и широко используется в различных областях, таких как физика, экономика, компьютерная графика и т. д.
Для выполнения умножения матриц необходимо соблюдать определенные правила:
- Число столбцов первой матрицы должно быть равно числу строк второй матрицы.
- Результирующая матрица будет иметь размерность, равную числу строк первой матрицы и числу столбцов второй матрицы.
- Элементы новой матрицы получаются путем суммирования произведений соответствующих элементов из строк первой матрицы и столбцов второй матрицы.
Умножение матриц может быть осуществлено как для матриц одинаковой размерности, так и для матриц разных размеров. В случае матриц разных размеров, умножение может быть выполнено только, если число столбцов первой матрицы равно числу строк второй матрицы.
Возможность умножения матриц разных размеров
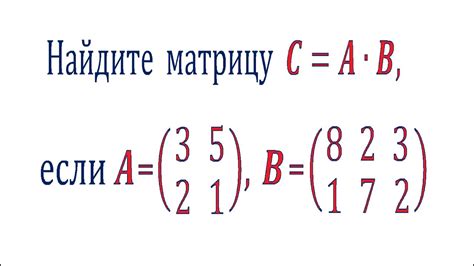
Для того чтобы умножить матрицы разных размеров, необходимо выполнение двух условий:
- Число столбцов первой матрицы должно быть равно числу строк второй матрицы. Только в этом случае операция умножения будет выполнима.
- Размеры итоговой матрицы будут определяться количеством строк первой матрицы и количеством столбцов второй матрицы. То есть, если первая матрица имеет размерность m x n, а вторая матрица - размерность n x p, то итоговая матрица будет иметь размерность m x p.
В результате умножения матриц разных размеров получается новая матрица, где каждый элемент рассчитывается путем перемножения соответствующих элементов исходных матриц и их суммирования.
Это полезное математическое свойство умножения матриц разных размеров применяется в различных областях, таких как линейная алгебра, статистика, физика и информатика.
Однако, следует помнить, что умножение матриц разных размеров является исключением из правила и требует дополнительной проверки размерностей для выполнения корректной математической операции.
Размерность матрицы и ее влияние на умножение

Умножение матриц разных размерностей возможно, но их размерности должны быть согласованы. При умножении матрицы A размерности m × n на матрицу B размерности n × p, получится матрица C размерности m × p. Количество столбцов матрицы A должно соответствовать количеству строк матрицы B, чтобы операция умножения была выполнима. В противном случае, умножение невозможно.
Размерность матрицы оказывает влияние на результат умножения. Если размерности матриц не согласованы, операция умножения не будет выполнима. Возможность умножения матриц разных размерностей позволяет решать разнообразные задачи, такие как линейное программирование, системы линейных уравнений и многое другое.
Применение операции умножения матриц разных размерностей требует внимательного анализа размерностей матриц и их соответствия. Использование матриц разных размерностей может быть полезным при решении сложных задач и моделировании различных процессов.
Алгоритм умножения матриц разных размеров

Умножение матриц разных размеров возможно с использованием специального алгоритма. Для этого необходимо учесть следующие шаги:
- Проверить совместимость матриц. При умножении матрицы A размером m на n на матрицу B размером n на k, количество столбцов в матрице A должно быть равно количеству строк в матрице B.
- Проинициализировать результирующую матрицу C размером m на k, где каждый элемент матрицы C равен нулю.
- Выполнить перемножение матриц. Для каждого элемента C[i][j] результирующей матрицы C вычислить сумму произведений элементов i-й строки матрицы A на элементы j-го столбца матрицы B.
- Записать полученные значения в результирующую матрицу C.
Процесс умножения матрицы A на матрицу B может быть представлен следующей формулой:
C[i][j] = A[i][1]*B[1][j] + A[i][2]*B[2][j] + ... + A[i][n]*B[n][j]
В результате выполнения всех шагов получается результирующая матрица C, размером m на k, которая является результатом умножения матриц A и B.
Применение умножения матриц разных размеров в реальной жизни
Одним из примеров использования умножения матриц разных размеров является компьютерная графика. В компьютерных программах для создания трехмерных моделей и визуализации объектов используются матрицы, которые описывают положение и изменение объектов в пространстве. Умножение матриц разных размеров позволяет комбинировать различные преобразования объектов, такие как масштабирование, поворот и сдвиг, и определять итоговую матрицу, которая описывает положение и форму объекта.
Еще одним примером использования умножения матриц разных размеров является анализ данных. В области бизнеса и науки часто возникает необходимость обработки больших массивов информации. Умножение матриц разных размеров можно использовать для вычисления скалярных произведений векторов и получения статистических характеристик данных, таких как корреляция и ковариация.
Использование умножения матриц разных размеров расширяет возможности математических моделей и позволяет анализировать сложные системы в различных областях нашей жизни. Понимание этой операции и ее применения помогает разрабатывать новые методы и алгоритмы для решения сложных задач и улучшения процессов в различных отраслях.
| Матрица A | Матрица B | Матрица C = A * B | |
|---|---|---|---|
| Размерность | m x n | n x p | m x p |
| Пример применения | Моделирование трехмерных объектов | Анализ данных | Вычисление координат объекта после преобразования |
Ключевые факторы при умножении матриц разных размеров

Умножение матриц разных размеров возможно, однако, сложность процесса возрастает и требует участия нескольких ключевых факторов. Вот некоторые из них:
1. Размерность матриц
Первым ключевым фактором является размерность матриц. Для умножения матрицы A на матрицу B, необходимо, чтобы количество столбцов матрицы A было равно количеству строк матрицы B. Если это условие не выполняется, умножение будет невозможно.
2. Корректное вычисление элементов
Вторым ключевым фактором является корректное вычисление элементов при умножении матриц. При умножении элементов матриц A и B получается новый элемент матрицы C. Элемент матрицы C находится путем умножения соответствующих элементов строк матрицы A на соответствующие элементы столбцов матрицы B и их последующего суммирования.
3. Размер результирующей матрицы
Третьим ключевым фактором является размер результирующей матрицы. Размерность результирующей матрицы будет определяться количеством строк матрицы A и количеством столбцов матрицы B. Если матрица A имеет размерность m x n, а матрица B имеет размерность n x p, то результирующая матрица C будет иметь размерность m x p.
Преимущества и ограничения умножения матриц разных размеров
Преимущества:
1. Расширение возможностей вычислений. Умножение матриц разных размеров позволяет решать более сложные задачи и моделировать более сложные системы. При использовании матричных операций с различными размерами матриц можно выражать более сложные математические и физические взаимосвязи.
2. Более гибкая и компактная запись вычислений. Умножение матриц разных размеров позволяет свести к минимуму количество записей и упростить вычисления, особенно при работе с большими объемами данных. Матричное умножение удобно применять при работе с большими системами линейных уравнений или при анализе больших наборов данных.
3. Возможность вычисления перемножения матриц с разными размерами. Если одна матрица имеет размерность m x n, а другая - n x p, результатом умножения будет матрица размерности m x p. Это позволяет получить информацию о связи между значениями элементов матриц разных размеров и использовать ее для дальнейших расчетов.
Ограничения:
1. Несоответствие размеров матриц. Для умножения матриц разных размеров необходимо, чтобы количество столбцов первой матрицы совпадало с количеством строк второй матрицы. В противном случае операция умножения не определена.
2. Затратность по времени и ресурсам. Умножение матриц разных размеров может быть более затратным по времени и требовать большего объема памяти. Чем больше размерность матриц, тем больше операций необходимо выполнить и больше памяти потребуется для хранения результатов.
3. Ограниченные применения. Умножение матриц разных размеров наиболее полезно при работе с линейными уравнениями, системами уравнений и алгебраическими моделями. В других случаях, где нет явной математической связи, результаты умножения матриц разных размеров могут быть неинформативными или не иметь практического значения.