При решении неравенств часто возникает вопрос о необходимости убирать знаменатель. Знание правил и умение применять их в различных ситуациях играют важную роль в решении математических задач. В данной статье мы рассмотрим условия, при которых можно убрать знаменатель в неравенстве, и приведем примеры, чтобы проиллюстрировать эти правила.
Первое правило гласит: если знаменатель положителен, то неравенство не меняет свою направленность при убирании знаменателя. То есть, если у нас есть неравенство a/b < c, где b - положительное число, то мы можем убрать знаменатель и получить эквивалентное неравенство a < b * c.
Однако, стоит помнить, что если знаменатель отрицателен, то направленность неравенства меняется при убирании знаменателя. Если у нас есть неравенство a/b < c, где b - отрицательное число, то при убирании знаменателя мы получаем неравенство a > b * c.
Что значит убрать знаменатель в неравенстве?

Убрать знаменатель в неравенстве означает преобразовать неравенство так, чтобы знаменатель, то есть знак "деления", исчез из выражения. Это позволяет упростить неравенство, делать его более легким для анализа и решения.
При убирании знаменателя в неравенстве необходимо учесть некоторые правила:
1. Убрать знаменатель, домножив обе части неравенства на значение знаменателя
Если знаменатель положительный, то неравенство не меняет своего направления:
а/b < c (при b > 0)
аб - c
Если знаменатель отрицательный, то направление неравенства должно поменяться:
а/b < c (при b < 0)
аб - c
2. Проверить знаки
После убирания знаменателя следует проверить знаки расположенных рядом чисел и знаки в получившемся неравенстве. Если числа оказываются различного знака, то получившееся неравенство верное. Если числа одного знака, то следует изменить направление неравенства.
Важно помнить, что при убирании знаменателя нужно быть аккуратным и тщательно следить за каждым шагом. Необходимо также обратить внимание на допустимые значения переменных и возможные исключения из уравнения.
Определение задачи и основные понятия

Задача состоит в том, чтобы привести неравенство к более простому виду, чтобы упростить его решение или анализ. При убирании знаменателя могут использоваться следующие основные понятия:
Умножение на положительное число: Если мы умножаем обе части неравенства на положительное число, то направление неравенства сохраняется.
Умножение на отрицательное число: Если мы умножаем обе части неравенства на отрицательное число, то направление неравенства меняется на противоположное.
Деление на положительное число: Если мы делим обе части неравенства на положительное число, то направление неравенства сохраняется.
Деление на отрицательное число: Если мы делим обе части неравенства на отрицательное число, то направление неравенства меняется на противоположное.
Эти правила позволяют нам избавиться от знаменателя в неравенстве и упростить его для дальнейшего решения или анализа.
Правило 1: Убираем знаменатель при умножении на положительное число

a/b < c,
где a, b и c - действительные числа, причем b > 0 и c > 0, то мы можем умножить обе части неравенства на b без изменения знака. В результате получим:
a < b * c.
Таким образом, убрав знаменатель, мы сможем более просто решить и интерпретировать данное неравенство. Используя данное правило, мы можем применить алгебраические операции и свойства чисел для дальнейшего упрощения и решения неравенства.
Пример 1: Раскрытие знаменателя и упрощение неравенства

Допустим, у нас есть неравенство:
2(x - 1) > 3(x + 2)
Чтобы убрать знаменатель в этом неравенстве, мы сначала умножим обе стороны неравенства на общий знаменатель, в данном случае это будет 6:
6 * 2(x - 1) > 6 * 3(x + 2)
После раскрытия скобок, получим:
12x - 12 > 18x + 36
Затем мы переносим все переменные на одну сторону неравенства, а все числа на другую сторону:
12x - 18x > 36 + 12
-6x > 48
Далее, чтобы получить значение переменной x, деля обе стороны неравенства на -6, нужно изменить направление неравенства, так как мы делим на отрицательное число:
(Заметьте, что при изменении направления неравенства, знак также меняется)
x < -8
Таким образом, решением данного неравенства будет набор всех значений x, меньших -8.
Правило 2: Убираем знаменатель при умножении на отрицательное число с изменением знака

Если в неравенстве присутствует знаменатель, то его можно убрать при умножении на отрицательное число, однако необходимо помнить, что при этом меняется направление неравенства.
Для наглядности рассмотрим пример:
| Исходное неравенство | Убираем знаменатель |
|---|---|
| \(\frac{a}{b} < c\) | \(a > bc\) |
Если мы умножаем исходное неравенство на отрицательное число, то при этом меняется направление неравенства. Например:
| Исходное неравенство | Убираем знаменатель и меняем знак |
|---|---|
| \(\frac{3}{2} < 4\) | \(-3 > -8\) |
Таким образом, при убирании знаменателя при умножении на отрицательное число, необходимо поменять направление неравенства.
Пример 2: Раскрытие знаменателя и изменение знака неравенства
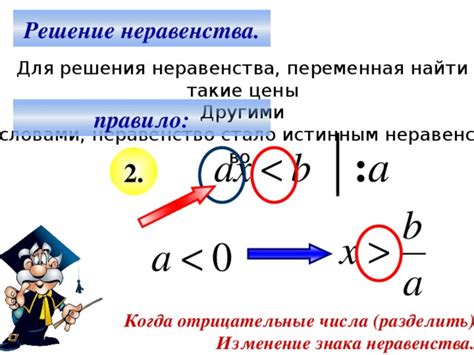
Часто в неравенствах возникает необходимость убрать знаменатель для упрощения вычислений. Рассмотрим пример и посмотрим, как можно применить данную технику.
Решим неравенство:
$$\frac{2}{x} < 5$$
Для начала, нужно удалить знаменатель. Один из вариантов - умножить обе части неравенства на знаменатель:
$$x \cdot \frac{2}{x} < 5 \cdot x$$
Получаем:
$$2 < 5x$$
Затем, как в обычном неравенстве, переносим все переменные на одну сторону, а числа на другую:
$$5x - 2 > 0$$
Теперь мы можем решать неравенство с одной переменной. Здесь важно помнить, что изменение знака неравенства происходит при умножении или делении обеих частей на отрицательное число:
- Если $5x - 2 > 0$, то $x > \frac{2}{5}$;
- Если $5x - 2 < 0$, то $x < \frac{2}{5}$.
Таким образом, получаем решение:
$$x > \frac{2}{5}$$
Правило 3: Убираем знаменатель, когда знаменатель и числитель имеют общий множитель

При решении неравенств со знаменателем важно запомнить правило, которое позволяет нам убрать знаменатель, если знаменатель и числитель имеют общий множитель.
Допустим, у нас есть неравенство а/б > с/d, где а, б, с и д - числа. Если числитель и знаменатель имеют общие множители, мы можем убрать их и переписать неравенство в более простой форме:
а/б > с/d
a * d > b * с
Пример:
Рассмотрим неравенство 2/x > 3/4. Заметим, что у числителя 2 есть общий множитель с числителем 3, а у знаменателя x - общий множитель с знаменателем 4. Мы можем убрать эти общие множители и решить неравенство следующим образом:
2/x > 3/4
2 * 4 > x * 3
8 > 3x
Теперь мы можем решить линейное неравенство 8 > 3x и найти значение x, чтобы удовлетворить данное неравенство.
Пример 3: Упрощение неравенства, имеющего общий множитель у знаменателя и числителя

Рассмотрим неравенство 2x/3 < 4/5. В данном случае у нас есть общий множитель у знаменателя и числителя, а именно число 3. Чтобы упростить это неравенство, мы можем умножить обе его стороны на 3.
Умножение на положительное число не меняет направление неравенства, поэтому мы получим: 2x < (4/5) * 3.
Далее, умножим дробь (4/5) на 3: 2x < (4/5) * 3 = 12/5.
Теперь наша задача - найти значение переменной x, удовлетворяющее этому неравенству. Для этого мы будем делить обе стороны неравенства на 2: (2x)/2 < (12/5)/2.
Это приведет нас к следующему: x < 6/5.