Понимание условий пересечения параллельных прямых является важным аспектом в геометрии. Параллельные прямые - это прямые, которые находятся в одной плоскости и никогда не пересекаются. Однако, в некоторых случаях параллельные прямые могут пересечься или становиться перпендикулярными. Для того чтобы определить, пересекаются ли две параллельные прямые, нужно применять определенные правила и методы.
Одним из основных условий пересечения параллельных прямых является то, что они должны находиться в одной плоскости. Если прямые находятся в разных плоскостях, то они могут быть сколь угодно близко друг к другу, но никогда не пересекутся. Плоскости могут быть вертикальными, горизонтальными или наклонными.
Еще одним важным условием является то, что у двух параллельных прямых должна быть общая точка. Это означает, что каждая из прямых должна иметь координаты, либо точку пересечения. Если две прямые имеют разные координаты и не имеют общей точки, то они не пересекаются, даже если они выглядят очень близко друг к другу.
В данной статье мы рассмотрим примеры условий пересечения параллельных прямых и дадим наглядное объяснение с применением соответствующих формул и правил. Также мы узнаем, как определить, пересекаются ли две параллельные прямые по данным координатам и какие могут быть исключения.
Условия пересечения параллельных прямых
Однако, в некоторых геометрических системах, можно представить условия, при которых параллельные прямые могут пересекаться. Например, в неевклидовой геометрии, такой как сферическая геометрия или геометрия на плоскости с отогнутыми краями. В таких системах геометрии параллельные прямые могут пересекаться в одной или более точках.
Если говорить о классической евклидовой геометрии, то существует несколько условий, при которых параллельные прямые могут прикинуться пересекающимися. Например, при использовании перспективной проекции либо при наложении на них другой геометрической фигуры, такой как окружность.
Однако было бы неправильным говорить, что параллельные прямые пересекаются в контексте евклидовой геометрии. По определению, они никогда не пересекаются. Возможные пересечения параллельных прямых следует рассматривать в контексте других геометрических систем, где основные правила и аксиомы могут меняться.
Правила и примеры

Для определения условий пересечения параллельных прямых существуют следующие правила:
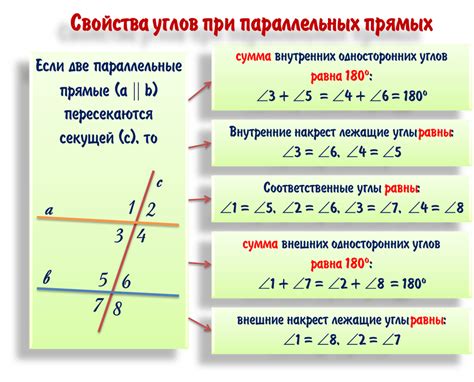
- Если две прямые параллельны и пересекаются с другой прямой, то углы, образованные при пересечении с этой прямой, будут равны между собой.
- Если две прямые параллельны и пересекаются с трансверсальной прямой, то смежные углы будут дополнительными
- Если две прямые параллельны и пересекаются с накрест лежащимися прямыми, то «внутренние» углы будут смежными, а "внешние" – дополнительными
Вот несколько примеров, чтобы помочь вам лучше понять эти правила:
Пример 1:
Даны две параллельные прямые a и b, и третья прямая c, пересекающая их.
Углы A и B образованные при пересечении прямой c с прямой a равны между собой, то есть A = B.
Пример 2:
Даны две параллельные прямые d и e, и трансверсальная прямая f, пересекающая их.
Углы А и В, образованные при пересечении прямой f с прямой d, являются смежными, то есть А + В = 180°.
Пример 3:
Даны две параллельные прямые g и h, и накрест лежащие прямые i и j, пересекающие их.
Углы P, Q, R и S образованные при пересечении прямых i и j с прямыми g и h, соответственно, имеют следующие связи:
- Углы P и Q являются смежными.
- Углы Q и R являются смежными.
- Углы R и S являются смежными.
- Углы P и S являются дополнительными.
Надеюсь, эти правила и примеры помогут вам лучше понять условия пересечения параллельных прямых.