Равносильность неравенств представляет собой важный аспект алгебры и математического анализа. Понимание процесса установки такой равносильности позволяет определить объем и характер решений системы неравенств.
Рассмотрим систему неравенств: x² + 7x + 1 > 0 и x = 7 - 1/x. Цель состоит в поиске всех значений переменной x, при которых оба неравенства выполняются одновременно.
Для начала, давайте разберемся с первым неравенством: x² + 7x + 1 > 0. Для того чтобы определить значения x, при которых это неравенство выполняется, мы можем применить различные методы, такие как анализ графика функции или использование квадратного трехчлена.
С другой стороны, второе неравенство x = 7 - 1/x может быть преобразовано путем перемещения слагаемых и умножения обеих сторон на x, что приводит к уравнению x² = 7x - 1. Задача заключается в поиске всех значений x, при которых это уравнение имеет решение.
Анализ неравенства x^2 + 7x + 1 > 0
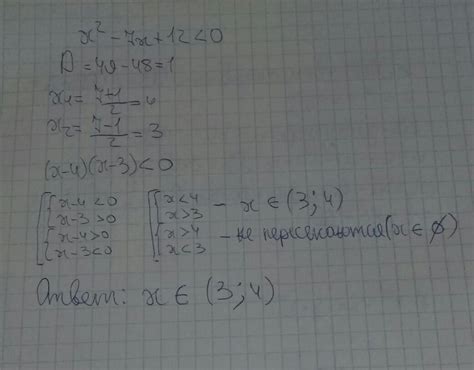
Для анализа данного неравенства нам необходимо найти все значения переменной x, при которых левая часть неравенства будет положительной.
Вначале рассмотрим дискриминант квадратного трёхчлена x^2 + 7x + 1:
Дискриминант D = b^2 - 4ac
где a = 1, b = 7, c = 1
Подставим значения:
D = 7^2 - 4 * 1 * 1 = 49 - 4 = 45
Таким образом, дискриминант равен 45.
Если дискриминант положителен, то уравнение имеет два различных действительных корня, а в нашем случае два различных действительных решения.
Далее найдём корни квадратного трёхчлена, решив квадратное уравнение
x1,2 = (-b +/- √D) / (2a)
Подставим значения:
x1,2 = (-7 +/- √45) / 2
Теперь, зная корни уравнения, мы можем построить график функции и проанализировать неравенство.
На графике квадратного трёхчлена видно, что функция меняет знак отрицательный на положительный при x < x1 и от положительного на отрицательный при x > x2.
Таким образом, решениями неравенства x^2 + 7x + 1 > 0 являются все значения x, лежащие в интервале (x1, x2).
Анализ равенства x = 7 - 1/x
Предположим, что x ≠ 0, чтобы избежать деления на ноль. Тогда мы можем умножить обе части уравнения на x, чтобы избавиться от дроби в правой части:
| Шаг | Выражение |
|---|---|
| 1 | x = 7 - 1/x |
| 2 | x^2 = 7x - 1 |
| 3 | x^2 - 7x + 1 = 0 |
Таким образом, мы получаем квадратное уравнение x^2 - 7x + 1 = 0. Мы можем найти его решения с использованием квадратного корня или метода факторизации. Решения этого уравнения могут дать нам полезную информацию о значениях x, которые удовлетворяют равенству x = 7 - 1/x.
Если рассмотреть график функции y = x^2 - 7x + 1, то можно заметить, что она представляет собой параболу с ветвями, направленными вверх. Таким образом, уравнение имеет два решения, которые представляют собой пересечения графика с осью x.
Доказательство равносильности неравенств
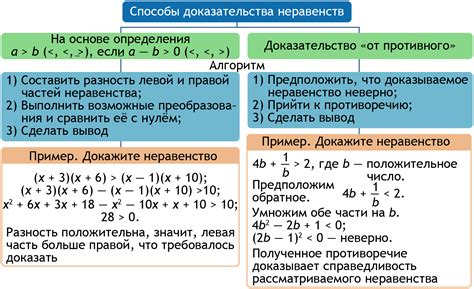
Для доказательства равносильности неравенств необходимо провести следующие шаги:
- Решить первое неравенство x^2 + 7x + 1 > 0. Неравенство является квадратным трехчленом, поэтому его можно решить с помощью метода дискриминанта или графически. Находим корни уравнения и определяем интервалы, на которых неравенство выполняется.
- Решить второе неравенство x = 7 - 1/x. Для этого нужно сначала избавиться от дроби, перемещая члены уравнения в одну сторону и приводя его к квадратному виду. Затем решить полученное квадратное уравнение и найти его корни.
- Сравнить интервалы, полученные при решении обоих неравенств. Если они совпадают, значит, неравенства равносильны. Если интервалы не совпадают, значит, неравенства не равносильны.
Таким образом, проведя указанные выше шаги, мы можем доказать равносильность или неравносильность данных неравенств.
Методы решения неравенства x^2 + 7x + 1 > 0 и равенства x = 7 - 1/x
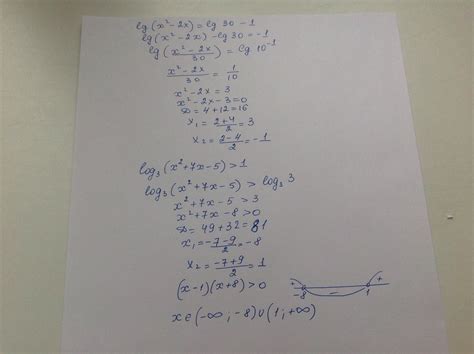
Решение равенства x = 7 - 1/x можно получить с помощью метода подстановки или метода приведения к квадратному уравнению. В первом случае подставляем x в исходное равенство и сокращаем, пока не получим уравнение, которое можно решить алгебраически. Во втором случае умножаем обе части уравнения на x и приводим его к квадратному виду. Затем решаем полученное квадратное уравнение и найденные корни проверяем в исходном равенстве.
Проверка корректности полученных решений
- Графический метод. Строим графики функций y = x^2 + 7x + 1 и y = 7 - 1/x и находим точки пересечения с осью абсцисс. Если полученные значения x совпадают с решениями, то решения корректны.
- Аналитический метод. Подставляем полученные значения x в исходные неравенства и проверяем их истинность. Если неравенство выполняется, то решение корректно.
- Численный метод. Для многочлена x^2 + 7x + 1 > 0 можно вычислить значения многочлена для полученных значений x. Если значение больше нуля, то решение корректно.
Важно помнить, что каждый из методов имеет свои ограничения и особенности, поэтому рекомендуется использовать несколько методов для проверки корректности полученных решений.
Примеры применения установки равносильности неравенств

Рассмотрим примеры применения установки равносильности неравенств для уравнений:
1. Решим неравенство x^2 + 7x + 1 > 0. Применим установку равносильности, заменив неравенство на эквивалентное уравнение x^2 + 7x + 1 = 0. Затем найдем корни этого уравнения и определим знаки между ними, чтобы получить окончательное решение неравенства.
2. Рассмотрим уравнение x = 7 - 1/x. Применим установку равносильности, заменив уравнение на эквивалентное неравенство x - 7 + 1/x = 0. Далее, найдем корни этого неравенства и определим интервалы, на которых оно принимает положительные значения, чтобы получить окончательное решение задачи.
Таким образом, применение установки равносильности неравенств позволяет упростить именно решение неравенств и уравнений, помогая найти значения переменных, удовлетворяющих заданному условию задачи.