Установка вида формулы по таблице истинности – важный шаг в процессе анализа логических выражений. Метод позволяет превратить набор данных о значениях истинности переменных в явное представление логической функции. Грамотное использование этого метода позволяет легко и быстро определить логические свойства и закономерности, скрытые за таблицей истинности.
Для того чтобы успешно установить вид формулы по таблице истинности, необходимо владеть базовыми знаниями алгебры логики, а также быть ознакомленным с правилами преобразования логических выражений. Эта техника может использоваться в самых разных сферах, начиная от разработки программного обеспечения и конструирования вычислительных схем, и заканчивая анализом данных в научных исследованиях и прогнозировании тенденций в экономике.
В данной статье вы найдете подробное руководство по установке вида формулы по таблице истинности, описание основных шагов и применяемых методов. Мы предоставим примеры и иллюстрации для наглядного представления процесса. Будьте готовы развить свои навыки работы с логическими выражениями и узнать новые способы анализа таблиц истинности!
Установка вида формулы по таблице истинности
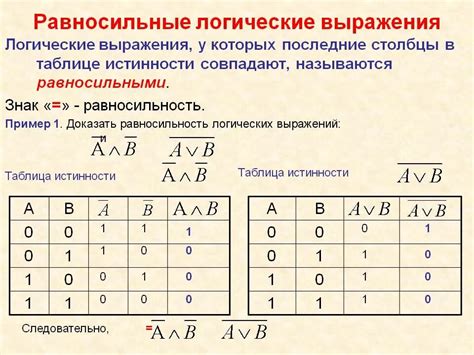
Формулы в логике представляют собой выражения, содержащие переменные и логические операции, такие как "и", "или" и "не". Чтобы правильно определить вид формулы по её таблице истинности, следует выполнить следующие шаги:
- Определить количество переменных в формуле. Для этого нужно посмотреть на таблицу истинности и посчитать количество столбцов, исключая столбец с результатом выражения. Например, если в таблице 4 столбца, значит формула содержит 3 переменные.
- Определить количество строк в таблице истинности. Это позволит определить, сколько значений может принимать каждая переменная. Если таблица истинности содержит 2 строки, значит каждая переменная может принимать 2 разных значений - либо истину, либо ложь.
- Записать выражение для каждой строки таблицы истинности. Для этого нужно посмотреть на значения переменных в каждой строке и выписать соответствующие им логические операции. Например, если переменная A имеет значение истины (1), переменная B имеет значение лжи (0) и переменная C имеет значение истины (1), то формула может выглядеть как A * (не B) + C.
- Объединить выражения для каждой строки таблицы истинности, используя логические операции. Например, если для первой строки формулой является A * (не B) + C, а для второй строки - (не A) + (не B) + C, то весь вид формулы может быть записан как (A * (не B) + C) или ((не A) + (не B) + C).
Используя данное руководство, вы сможете установить вид формулы по таблице истинности и корректно записать её с использованием переменных и логических операций.
Руководство по установке вида формулы по таблице истинности
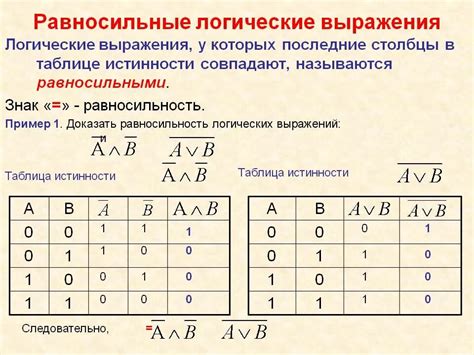
- Получите таблицу истинности для вашей формулы. В таблице должны быть указаны все возможные значения переменных и соответствующие им значения формулы.
- Определите количество и тип переменных в формуле. Это позволит вам правильно разделить таблицу истинности на соответствующие столбцы.
- Создайте заголовки для каждого столбца таблицы истинности. Заголовки должны содержать имена переменных, указанные в таблице.
- Заполните значениями каждый столбец таблицы истинности в соответствии с данными в таблице.
- Разбейте формулу на составляющие ее части: операторы, переменные и скобки.
- Используйте соответствующие символы для каждого типа частей формулы. Например, использование символа "&" для оператора "логическое И".
- Расставьте скобки для выделения приоритетных операций.
- Подставьте значения переменных вместо их имен в формулу.
- Проанализируйте полученную формулу и проверьте ее на соответствие данным в таблице истинности.
Следуя этим инструкциям, вы сможете установить внешний вид формулы по таблице истинности и легко понять ее смысл. Правильный вид формулы поможет вам выполнить дальнейшие операции с ней, такие как упрощение или построение схемы функции.
Примеры установки вида формулы по таблице истинности
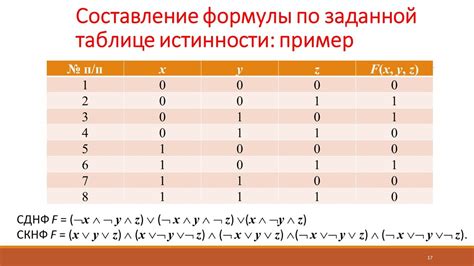
При решении логических задач зачастую требуется установить вид формулы по заданной таблице истинности. Для этого необходимо проанализировать значения переменных и связи между ними, чтобы определить какие логические операции использовать и в какой последовательности.
Например, рассмотрим таблицу истинности для формулы логики высказывания:
- A | B | C | F
- 0 | 0 | 0 | 1
- 1 | 0 | 0 | 0
- 0 | 1 | 0 | 0
- 1 | 1 | 1 | 1
Из этой таблицы видно, что результатом выражения F является 1, только когда все переменные A, B и C равны 0. Таким образом, можно записать формулу следующим образом: F = (¬A ∧ ¬B ∧ ¬C).
В другом примере, представленной таблицы истинности:
- P | Q | R | G
- 0 | 0 | 0 | 1
- 1 | 0 | 0 | 0
- 0 | 1 | 0 | 1
- 1 | 1 | 1 | 0
В этом случае видно, что результатом выражения G является 1, только когда переменные P и R равны 0, или переменные Q и R равны 1. Формулу можно записать так: G = ((¬P ∧ ¬R) ∨ (Q ∧ R)).
Подобным образом можно анализировать таблицы истинности различных выражений и определять их вид, используя логические операции (конъюнкция, дизъюнкция, отрицание и т.д.) и соответствующие условия.
Инструкции по установке вида формулы по таблице истинности
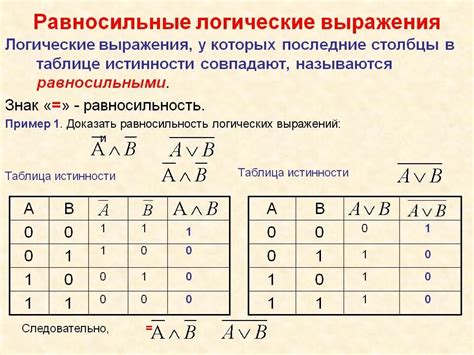
Для установки вида формулы по таблице истинности вам потребуется следовать следующим инструкциям:
- Соберите таблицу истинности, в которой указаны все возможные значения переменных и значение самой формулы для каждого набора переменных.
- Определите количество уникальных переменных в формуле.
- Создайте таблицу HTML с нужным количеством столбцов, равным количеству уникальных переменных плюс один столбец для значения формулы.
- В первой строке таблицы введите заголовки столбцов, соответствующие уникальным переменным плюс заголовок для значения формулы.
- Заполните остальные строки таблицы значениями переменных и соответствующим им значениям формулы.
- Разместите таблицу на странице с помощью тега <table>.
Пример таблицы истинности и соответствующей ей таблицы HTML:
| A | B | Формула |
|---|---|---|
| true | true | true |
| true | false | false |
| false | true | false |
| false | false | true |
В данном примере используются две переменные A и B, и формула принимает значение "true" или "false" в зависимости от значений переменных.