Друзья, наверняка у вас не раз возникал вопрос, как узнать диагональ куба по его площади. Не переживайте, в этой статье мы расскажем вам простое руководство и поделимся шагами, чтобы вы могли решить эту задачу без труда.
Во-первых, диагональ куба - это расстояние между двумя противоположными вершинами. Она может быть вычислена с использованием знания площади куба и некоторых математических формул. Но не беспокойтесь, вы не нуждаетесь в глубоких знаниях математики, чтобы справиться с этой задачей.
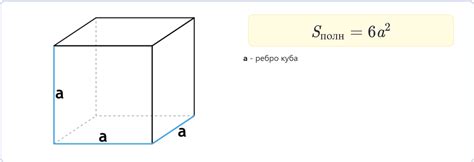
Шаг 1: Находим площадь куба. Площадь куба вычисляется по формуле: S = 6 * a^2, где а - длина стороны куба. Возведите длину стороны в квадрат и умножьте на 6. Полученный результат будет площадью куба.
Шаг 2: Используем формулу для нахождения диагонали. Диагональ куба можно выразить через его площадь по следующей формуле: d = √(3 * S), где d - диагональ куба, S - площадь куба.
Теперь, когда у вас есть формулы и простое руководство, вы можете легко вычислить диагональ куба по его площади. Не забывайте, что точные измерения и правильные расчеты являются основой для достижения верного результата.
Как узнать диагональ куба по площади: шаг за шагом
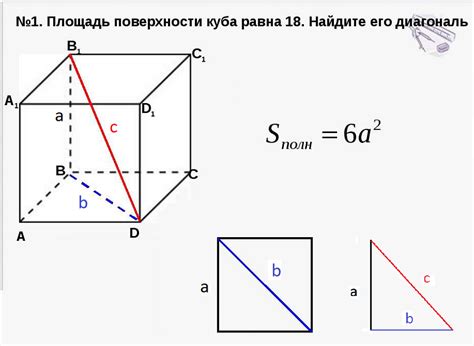
Шаг 1: Определите площадь одной боковой поверхности куба.
Для этого умножьте длину одной стороны куба на саму себя. Позволяет предположить, что длины всех сторон куба равны между собой, поэтому можно выбрать любую сторону для этого расчета. Обозначим длину стороны как "a". Тогда площадь одной боковой поверхности равна "a * a" или "a^2".
Шаг 2: Умножьте площадь одной боковой поверхности на 4.
Так как куб имеет 6 одинаковых боковых поверхностей, чтобы найти площадь всех боковых поверхностей, нужно умножить площадь одной боковой поверхности на 6. В нашем случае это будет равно "4 * a^2".
Шаг 3: Найдите длину ребра куба.
Используя полученную площадь всех боковых поверхностей, можно найти длину ребра куба. Для этого найдите квадратный корень из площади всех боковых поверхностей. Обозначим длину ребра как "s". Тогда уравнение будет выглядеть следующим образом: "s = √(4 * a^2)".
Шаг 4: Умножьте длину ребра на √3 (корень из 3).
Чтобы найти диагональ куба, нужно умножить длину ребра на корень из 3. Выражение будет выглядеть следующим образом: "d = s * √3".
Теперь, следуя этим шагам, вы можете легко узнать диагональ куба по известной площади.
Научитесь считать площадь грани куба
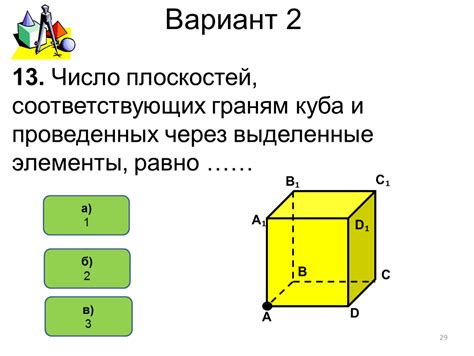
Формула для вычисления площади грани куба проста: S = a², где S – площадь грани, а a – длина ребра куба.
Как только у вас есть значение длины ребра куба, вы можете легко вычислить площадь грани. Просто возведите длину ребра в квадрат, и получите результат.
Например, если длина ребра куба равна 5 см, то площадь одной его грани будет составлять 25 см² (5² = 25).
Зная площадь грани куба, вы сможете далее использовать эту информацию для решения различных задач и задачек, связанных с изучением кубов и их свойств.
Узнайте формулу для вычисления диагонали куба из площади грани
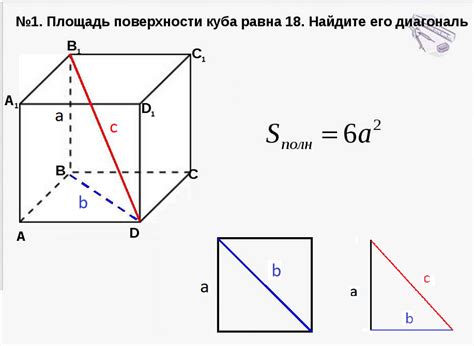
Формула для вычисления диагонали куба из площади грани выглядит так:
Диагональ = √(2 * (сторона ^ 2))
Где:
- Диагональ - длина диагонали куба
- Сторона - длина стороны куба
- ^ - знак возведения в степень
- √ - знак квадратного корня
Используя данную формулу, вы можете легко вычислить длину диагонали куба, зная только площадь его грани. Это может быть полезно, например, при решении задач связанных с геометрией или в строительстве.
Разберитесь, что такое площадь грани и как ее измерить
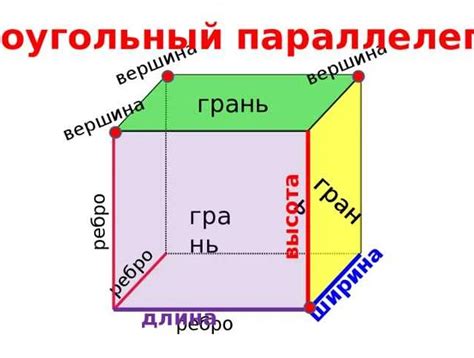
Определить площадь грани куба можно с помощью формулы:
| S = a2 |
Где S - площадь грани, а a - длина стороны куба.
Для измерения площади грани необходимо измерить длину одной из сторон куба с помощью линейки или мерной ленты. После этого длину стороны нужно возведенную в квадрат, используя указанную формулу.
Например, если длина стороны куба равна 10 см, то площадь грани будет:
| S = 102 = 100 см2 |
Таким образом, площадь грани куба равна 100 квадратным сантиметрам. Используя эту информацию, можно продолжить вычисления, чтобы найти диагональ куба по площади.
Подключите счетчик калькулятора и посчитайте площадь грани куба
После того, как вы узнали диагональ куба, вам может понадобиться рассчитать площадь его грани. Для этого вы можете воспользоваться калькулятором.
Калькулятор поможет вам быстро и точно рассчитать площадь грани куба. Для этого вам нужно ввести значение длины ребра куба в соответствующее поле и нажать кнопку "Рассчитать". Калькулятор автоматически выполнит математические операции и выведет результат на экран.
Площадь грани куба можно рассчитать по формуле:
S = a * a
- где S - площадь грани куба,
- a - длина ребра куба.
Например, если длина ребра куба равна 5 см, то вычисление будет выглядеть следующим образом:
S = 5 * 5 = 25 (см2)
Теперь вы можете легко рассчитать площадь грани куба с помощью калькулятора!
Вставьте значение площади грани в формулу вычисления диагонали
Для этого нам необходимо знать значение площади грани, которое мы обозначим как S. Формула для вычисления диагонали квадрата выглядит следующим образом:
d = √2S
Где d - диагональ квадрата, S - площадь грани. Чтобы вычислить диагональ куба по площади грани, просто подставьте значение площади грани вместо S в эту формулу.
Например, если площадь грани куба равна 25 квадратных единиц, то формула примет следующий вид:
d = √2 * 25
Раскрывая скобки и упрощая, получим:
d = √50
Чтобы найти точное значение диагонали, достаточно найти квадратный корень из 50:
d ≈ 7.07
Таким образом, диагональ куба, у которого площадь грани равна 25 квадратным единицам, примерно равна 7.07 единицам длины.
Проанализируйте полученный результат

Получение значения диагонали куба по известной площади может быть полезным при решении различных задач в геометрии и инженерии. Анализируя полученный результат, можно определить соотношение между площадью и диагональю куба, а также выявить закономерности и связи, которые могут быть полезными при работе с кубическими формами.
При анализе полученного результата можно обратить внимание на следующие аспекты:
- Увеличение площади куба приводит к увеличению его диагонали. Если два куба имеют одинаковую площадь, то диагональ более большего куба будет длиннее.
- Зная площадь и диагональ куба, можно оценить его объем и описать его характеристики. Например, можно сравнить объемы двух кубов с разными площадями и определить, какой из них более вместительный.
- Полученный результат помогает понять, как площадь поверхности куба влияет на его геометрические свойства. Чем больше площадь куба, тем более сложная его геометрия и структура.
- Анализ результатов также может помочь в определении применимости куба в различных сферах. Например, зная площадь и диагональ куба, можно определить, подойдет ли он для определенной задачи или требуется куб с другими характеристиками.
Важно отметить, что полученный результат является теоретическим и представляет идеализированный куб. В реальности могут существовать отклонения и неточности, связанные с изготовлением и измерением, которые необходимо учитывать при решении практических задач.