Периметр равнобедренной трапеции – это сумма длин всех ее сторон. Равнобедренная трапеция имеет две параллельные стороны, которые называются основаниями, и две равные прямые стороны, которые называются боковыми сторонами. Для нахождения периметра равнобедренной трапеции существует простая формула.
Формула для расчета периметра равнобедренной трапеции выглядит следующим образом:
Периметр = основание1 + основание2 + боковая сторона1 + боковая сторона2
Важно помнить, что длина оснований и боковых сторон должна быть измерена в одной и той же единице измерения (например, сантиметрах или метрах).
Давайте рассмотрим пример. Представим, что у нас есть равнобедренная трапеция с основаниями длиной 4 см и 8 см, а боковые стороны равны 6 см каждая. Чтобы найти периметр данной трапеции, мы просто подставляем известные значения в формулу:
Периметр = 4 см + 8 см + 6 см + 6 см = 24 см
Таким образом, периметр равнобедренной трапеции равен 24 см.
Значение периметра равнобедренной трапеции
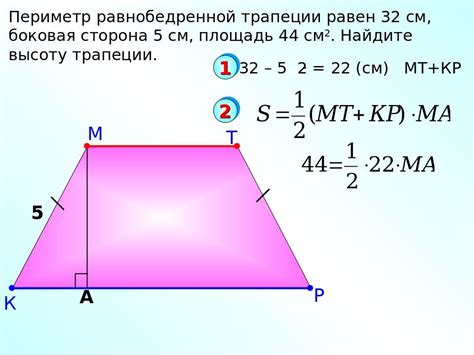
Для вычисления периметра равнобедренной трапеции можно использовать следующую формулу:
P = a + b + c + d
Где:
- a и b - равные стороны трапеции (основания);
- c и d - неравные стороны трапеции (боковые стороны).
Итак, чтобы найти периметр равнобедренной трапеции, нужно сложить длины ее оснований и длины обеих боковых сторон.
Зная значения этих сторон, можно легко вычислить периметр равнобедренной трапеции и использовать его в дальнейших расчетах или задачах.
Что такое равнобедренная трапеция
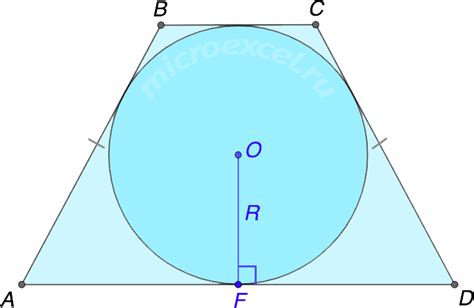
Такая трапеция имеет следующие составляющие элементы:
- две основания, которые являются параллельными отрезками
- две боковые стороны, которые равны между собой
- два угла при основаниях, которые равны между собой
- две диагонали, которые перпендикулярны между собой и делят трапецию на два треугольника.
Для нахождения периметра равнобедренной трапеции сначала нужно найти длины всех ее сторон. Затем периметр равнобедренной трапеции вычисляется как сумма длин всех сторон.
| Равнобедренная трапеция | |
| Основание a | Основание b |
| _____________________________ | |
| Боковая сторона c | Боковая сторона c |
| _____________________________ | |
| Периметр равнобедренной трапеции: P = a + b + 2c | |
Формула для нахождения периметра

Периметр равнобедренной трапеции можно найти, используя следующую формулу:
- Определите длины оснований трапеции.
- Найдите длину боковой стороны, соединяющей вершины оснований.
- Сложите длины всех сторон, чтобы получить периметр.
Формула для периметра равнобедренной трапеции выглядит следующим образом:
Периметр = длина первого основания + длина второго основания + 2 * длина боковой стороны
Например, если первое основание равно 5 см, второе основание равно 7 см, а длина боковой стороны равна 4 см, то периметр равнобедренной трапеции будет:
Периметр = 5 см + 7 см + 2 * 4 см = 20 см
Используя данную формулу, вы можете легко найти периметр любой равнобедренной трапеции, зная длины её оснований и боковую сторону.
Примеры вычисления периметра

Рассмотрим несколько примеров вычисления периметра равнобедренной трапеции.
Пример 1:
Дана равнобедренная трапеция со сторонами a = 8 см, b = 6 см и высотой h = 4 см. Для вычисления периметра воспользуемся формулой:
периметр = a + b + 2 * c,
где c - боковая сторона трапеции. В данном случае, c = √((a - b/2)^2 + h^2) = √((8 - 6/2)^2 + 4^2) = √((8 - 3)^2 + 16) = √(5^2 + 16) = √(25 + 16) = √41 ≈ 6.40 см.
Тогда периметр равнобедренной трапеции равен:
периметр = 8 + 6 + 2 * 6.40 = 8 + 6 + 12.80 = 26.80 см.
Пример 2:
Дана равнобедренная трапеция со сторонами a = 12 м, b = 9 м и высотой h = 5 м. Используем формулу для вычисления периметра:
периметр = a + b + 2 * c,
где c - боковая сторона трапеции. В данном случае, c = √((a - b/2)^2 + h^2) = √((12 - 9/2)^2 + 5^2) = √((12 - 4.5)^2 + 25) = √(7.5^2 + 25) = √(56.25 + 25) = √81.25 ≈ 9 м.
Тогда периметр равнобедренной трапеции равен:
периметр = 12 + 9 + 2 * 9 = 12 + 9 + 18 = 39 м.
Таким образом, можно вычислить периметр равнобедренной трапеции, зная ее стороны и высоту по данной формуле. Помните, что всякий раз при использовании формулы необходимо проверить правильность подстановки значений и провести расчеты с точностью.
Области применения равнобедренной трапеции
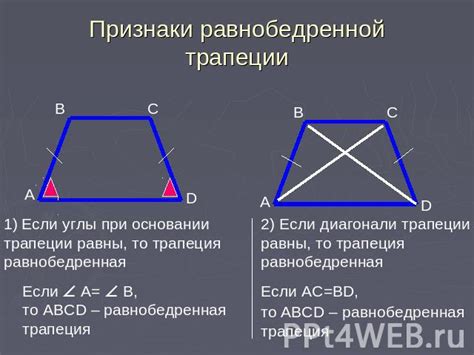
Одной из областей применения равнобедренной трапеции является геометрия. Обозначение геометрических фигур часто основывается на их характеристиках, и равнобедренная трапеция – не исключение. Геометрические задачи, которые описывают равнобедренные трапеции, могут быть полезны при решении других задач, связанных с данными фигурами.
Также равнобедренная трапеция может использоваться в архитектуре. Ее графическое изображение может использоваться при проектировании зданий и сооружений. Форма равнобедренной трапеции может быть использована для создания стильных фасадов или оконных откосов.
В области градостроительства равнобедренная трапеция может использоваться для планировки территории. Форма равнобедренной трапеции позволяет максимально эффективно использовать пространство и создать гармоничный архитектурный облик.
Также равнобедренные трапеции используются в промышленности, например, при создании деталей для машиностроения или конструкций для инженерных сооружений. Форма равнобедренной трапеции может обеспечивать определенную жесткость и прочность конструкций.
Таким образом, равнобедренная трапеция имеет широкие области применения в различных сферах, начиная от геометрии и заканчивая архитектурой и промышленностью. Знание особенностей и свойств равнобедренной трапеции может быть полезным для решения задач в различных областях науки и практики.