Синус угла треугольника - это отношение противоположного катета к гипотенузе. Когда мы знаем значения катетов, мы можем использовать их, чтобы найти значение синуса угла.
Для этого нам понадобится знание основных математических формул и правил. Итак, предположим, у нас есть прямоугольный треугольник с известными катетами. Мы помним, что гипотенуза - это главная сторона треугольника, а синус угла - это отношение противоположного катета к гипотенузе.
Чтобы найти синус угла, нам нужно разделить длину противоположного катета на длину гипотенузы. Таким образом, мы получим значение синуса угла в виде десятичной дроби. Зная значения катетов и используя эту формулу, мы сможем точно найти синус угла треугольника.
Что такое синус угла треугольника?
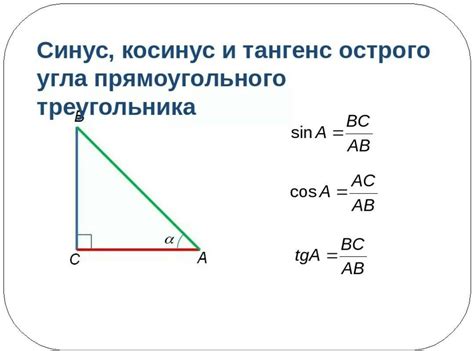
Синус угла можно определить как отношение противоположного катета к гипотенузе:
sin(A) = a / c
где A - угол, a - противоположный катет и c - гипотенуза.
Синус угла является одним из трех основных тригонометрических отношений в математике, вместе с косинусом и тангенсом.
Синус угла треугольника имеет множество применений в различных областях, включая геометрию, физику, инженерию, компьютерную графику и много других. Например, синус угла может использоваться для вычисления высоты объекта или расчета силы, действующей на тело под углом.
Определение синуса угла треугольника
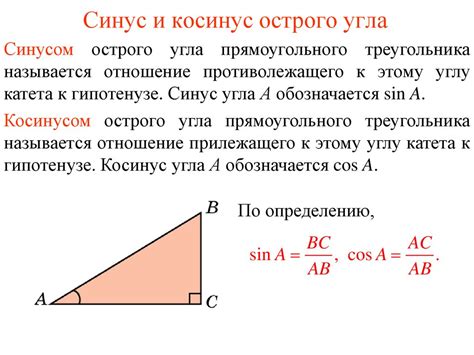
Sin(A) = ОпPOSITE / HYPOTENUSE
где:
- Sin(A) - значение синуса угла A;
- ОPPSITE - длина противолежащего катета;
- HYPOTENUSE - длина гипотенузы треугольника.
Зная значения противолежащего катета и гипотенузы, можно легко вычислить синус угла треугольника, используя формулу выше. Значение синуса всегда будет находиться в диапазоне от -1 до 1. Отрицательное значение синуса указывает на то, что угол находится во втором или третьем квадранте, тогда как положительное значение синуса указывает на то, что угол находится в первом или четвертом квадранте.
Определение синуса угла треугольника позволяет нам вычислить его значение и использовать его в дальнейших математических расчетах или геометрических построениях.
Как найти синус угла треугольника
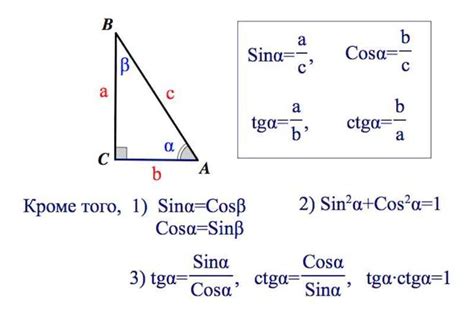
Синус угла треугольника можно найти, зная длины его сторон или отношение катетов. Если вам известны катеты треугольника, то для нахождения синуса угла можно воспользоваться теоремой Пифагора. Если же вам известны отношения катетов треугольника, то можно воспользоваться формулой синуса.
1. Если вам известны катеты треугольника и вы хотите найти синус угла, то следуйте этим шагам:
- Воспользуйтесь теоремой Пифагора, чтобы найти гипотенузу треугольника.
- Разделите длину катета, смежного с углом, на гипотенузу.
- Полученное значение будет синусом искомого угла треугольника.
Например, если в треугольнике катеты равны 3 и 4, а вы хотите найти синус угла, смежного с катетом длиной 4, вычислите:
sin(угол) = 4 / √(3²+4²) = 4 / 5 = 0.8
Таким образом, синус угла будет равен 0.8.
2. Если вам известны отношения катетов треугольника, вы можете воспользоваться формулой синуса:
- Разделите длину катета, смежного с углом, на длину другого катета.
- Полученное значение будет синусом искомого угла треугольника.
Например, если у вас есть треугольник, в котором отношение катетов равно 3/4, и вы хотите найти синус угла, смежного с катетом, длина которого равна 4, вычислите:
sin(угол) = 4 / 4 * 3 = 1 / 3 = 0.33
Таким образом, синус угла будет равен 0.33.
Метод 1: Используйте отношение катета к гипотенузе

Синус угла можно вычислить, используя отношение катета к гипотенузе в прямоугольном треугольнике. Для этого необходимо знать значения катетов треугольника.
Формула для вычисления синуса угла:
- Синус угла = (значение катета) / (значение гипотенузы)
Пример:
- Пусть значение первого катета равно 3
- Пусть значение второго катета равно 4
- Найдем значение гипотенузы с использованием теоремы Пифагора: гипотенуза^2 = первый катет^2 + второй катет^2
- гипотенуза^2 = 3^2 + 4^2 = 9 + 16 = 25
- гипотенуза = √25 = 5
- Теперь можно вычислить синус угла, используя формулу:
- Синус угла = (значение катета) / (значение гипотенузы)
- Синус угла = 4 / 5 = 0.8
Таким образом, при заданных значениях катетов 3 и 4, синус угла будет равен 0.8.
Метод 2: Используйте теорему Пифагора
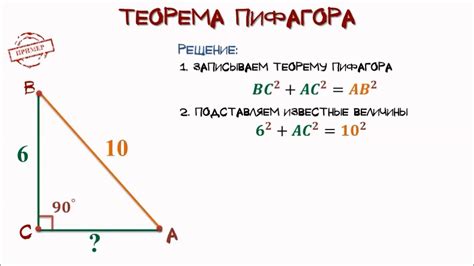
Если у нас заданы катеты треугольника, то можем найти гипотенузу с помощью этой теоремы. Далее, используя соотношение sin(угол) = противолежащий катет / гипотенуза, найдем синус угла треугольника.
Применение данного метода следует подходить, если известно, что угол треугольника является прямым - иначе теорема Пифагора не будет работать.
Давайте рассмотрим пример:
Пример:
У нас есть прямоугольный треугольник с катетами a = 4 и b = 3. Чтобы найти синус угла треугольника, мы можем использовать теорему Пифагора. Согласно теореме, гипотенуза c равна корню квадратному из суммы квадратов катетов: c = sqrt(a^2 + b^2) = sqrt(4^2 + 3^2) = sqrt(25) = 5. Теперь мы можем найти синус угла, используем формулу sin(угол) = противолежащий катет / гипотенуза: sin(угол) = a / c = 4 / 5 = 0.8.
Таким образом, синус угла этого треугольника равен 0.8.
Применение синуса угла треугольника
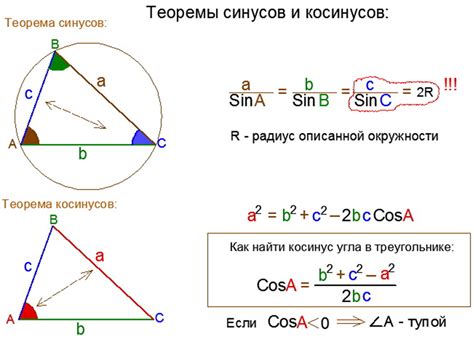
Применение синуса угла треугольника широко распространено в различных областях, включая физику, геометрию, строительство и медицину. Например, в физике синус угла используется для определения векторной составляющей силы, а в геометрии - для нахождения длины высоты треугольника.
Для еще большего удобства в расчетах существует таблица значений синусов углов от 0 до 90 градусов. Эта таблица может быть использована для быстрого определения синуса угла без необходимости выполнять сложные вычисления.
Важно отметить, что для использования синуса угла треугольника необходимо обладать знаниями о длинах катетов и гипотенузы треугольника. Эти данные можно получить из различных источников, таких как измерения или задачи с геометрическими формулами.
| Угол (градусы) | Синус угла |
|---|---|
| 0° | 0 |
| 30° | 0.5 |
| 45° | 0.707 |
| 60° | 0.866 |
| 90° | 1 |