Дроби - это одно из основных понятий математики, которое может вызывать сложности у многих людей. Однако, понимание того, как получить числитель и знаменатель дроби, может помочь упростить процесс работы с ними.
Числитель - это числовая часть дроби, которая находится над чертой. Он показывает, сколько частей от целого занимает дробь. Чтобы получить числитель дроби, необходимо обратить внимание на число, которое находится перед знаком дроби.
Например, если у нас есть дробь 3/4, то числитель этой дроби равен 3. Это означает, что дробь занимает 3 части от целого.
Знаменатель - это число, которое находится под чертой дроби. Он показывает, на сколько частей делится целое. Чтобы получить знаменатель дроби, необходимо обратить внимание на число, которое находится после знака дроби.
Например, в дроби 5/8 знаменатель равен 8. Это означает, что целое делится на 8 равных частей.
Знание числителя и знаменателя позволяет легче понять, как работать с дробями и выполнять операции с ними, такие как сложение, вычитание, умножение и деление.
Запомните эти простые способы получения числителя и знаменателя дробей и улучшите свои навыки в работе с этой важной математической концепцией.
Важность понимания дробей в математике

Разделение числа на числитель и знаменатель в дроби не только помогает нам представить дробное значение, но также позволяет более точно указывать, сколько частей из общего целого мы рассматриваем. Числитель указывает на количество частей, которые мы имеем, а знаменатель – на общее количество частей, на которое разделено целое.
Например:
В обычной жизни мы часто сталкиваемся с дробными значениями. Разделение пиццы на равные части, определение вероятности событий, решение задач на доли и проценты – все это требует понимания дробей. Дроби позволяют нам выражать и сравнивать значимость целей, доли и доли от долей, использовать математические операции для выполнения расчетов.
Понимание дробей также помогает развивать логическое мышление, умение анализировать и решать проблемы. Оно тесно связано с понятием пропорциональности и может быть ключевым фактором в решении задач на рост, масштабирование и оценку количества в различных ситуациях. Более того, уверенное владение дробями способствует развитию общей математической грамотности и увеличивает возможности в дальнейшем углубленном изучении математики.
В целом, понимание дробей является необходимым навыком не только в математике, но и в повседневной жизни, ведь они тесно связаны с рациональным мышлением, логикой и способностью адаптироваться к различным ситуациям. Основное внимание к дробям на начальных этапах обучения позволяет лучше освоить их концепцию и приобрести полезный инструмент для решения различных задач.
Простые способы получения числителей и знаменателей
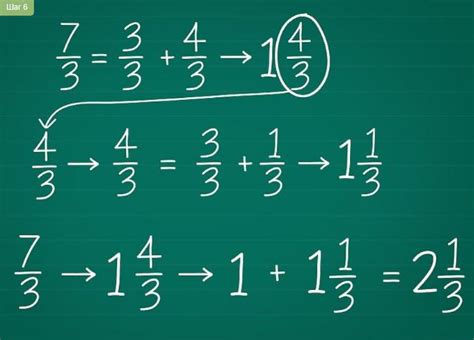
Существуют различные способы получения числителей и знаменателей дробей, которые могут быть полезны при работе с этими математическими конструкциями.
Один из самых простых способов получения числителя и знаменателя дроби – это разделение целого числа на части. Например, если у нас есть число 5, мы можем разделить его на две части: 2 и 3. Тогда получится дробь 2/3, где числитель равен 2, а знаменатель - 3.
Еще один способ получения числителей и знаменателей - это использование десятичных дробей. Для этого нужно разделить десятичное число на целую часть и дробную часть. Например, если у нас есть число 3.25, то 3 будет числителем, а 25 - знаменателем. Таким образом, получится дробь 3/25.
Другой простой способ получения числителей и знаменателей - это использование отношения двух чисел. Например, если у нас есть отношение 2:3, то 2 будет числителем, а 3 - знаменателем. Таким образом, получится дробь 2/3.
Иногда, для получения числителя и знаменателя, можно использовать простые математические операции, такие как сложение или вычитание. Например, если у нас есть задача на сложение двух чисел, то их сумма будет числителем, а знаменатель останется без изменений.
Важно помнить, что числитель и знаменатель дроби должны быть взаимно простыми числами, то есть не иметь общих делителей, кроме 1. В противном случае, дробь можно сократить, чтобы получить наименьшее представление.
Используя эти простые способы, вы можете легко получать числители и знаменатели дробей и справиться с математическими задачами, связанными с ними.
Примеры использования дробей в повседневной жизни
1. Кулинария: При приготовлении еды иногда необходимо использовать дроби, например, при измерении ингредиентов. Если рецепт требует половины чашки муки или трети столовой ложки сахара, то это является примером использования дробей.
2. Торговля: В магазинах и супермаркетах, цены могут быть представлены в виде десятичных дробей. Например, товар может стоить 9,99 доллара или 4,25 евро. Чтобы понять, сколько нужно заплатить, мы должны понимать, как работать с десятичными дробями.
3. Строительство и дизайн: В строительстве и дизайне дроби широко используются для измерения размеров и пропорций. Например, при планировании помещения или строящегося здания, важно учитывать отношение длины к ширине с помощью дробей.
4. Время: Понимание дробей также важно при работе с временем. Например, половина часа или треть минуты – это дробные значения времени. Когда мы говорим о времени, мы часто используем дроби, чтобы указать точное время.
5. Финансы: В области финансов дроби используются для расчета процентных ставок, вычисления доли доходов или убытков. Если у вас есть вклад в банке с 3/4 процента ежегодной ставки, то вы можете использовать дроби, чтобы понять, сколько денег вы получите в итоге.
Популярные методики обучения дробям

Обучение дробям может быть сложным процессом для многих детей. Однако, существуют различные методики, которые могут помочь им в понимании и усвоении этой математической концепции.
Одной из популярных методик является методика сравнения. В рамках этой методики детям предлагается сравнивать дроби между собой и определять, какая дробь больше или меньше. Это позволяет им визуализировать отношения между дробями и понять, какую часть целого они представляют.
Другой методикой является методика разделения. Детям предлагается разделять отрезки, фигуры или другие предметы на равные части и определять числитель и знаменатель дроби на основе этого разделения. Этот метод помогает им понять, как число может быть разделено на равные части и какие числа соответствуют числителю и знаменателю дроби.
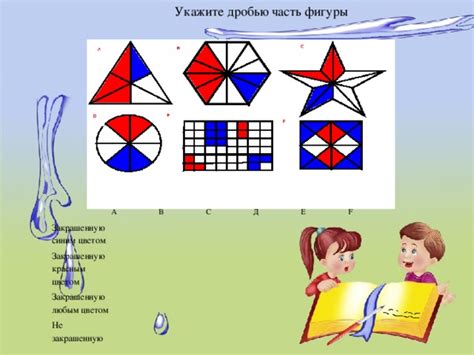
Также существует методика с помощью изобразительного искусства. В рамках этой методики детям предлагается использовать рисунки и диаграммы для визуализации дробей. Они могут создавать свои собственные диаграммы, закрашивая определенное количество частей и определяя числитель и знаменатель дроби на основе закрашенных и незакрашенных частей.
Некоторые методики использования игр и задач также могут помочь детям понять дроби. Игры, основанные на дробях, могут быть интересными и веселыми для детей, одновременно развивая их математические навыки. Задачи, связанные с реальными ситуациями, позволяют детям применить свои знания о дробях в практических ситуациях и укрепить их понимание этой математической концепции.
Важно заметить, что каждый ребенок может предпочитать разные методики обучения, поэтому важно использовать разнообразные подходы при обучении дробям и адаптировать их под конкретные потребности каждого ребенка.
Рекомендации для успешного освоения работы с дробями

Работа с дробями может доставить определенные трудности, особенно при первом знакомстве с этой темой. Однако, соблюдение ряда простых рекомендаций поможет успешно освоить работу с дробями и правильно выполнять операции с числителями и знаменателями.
1. Правильно запишите дроби. Удостоверьтесь, что числитель и знаменатель разделяются прямой чертой и корректно записаны. Будьте внимательны при вводе длинных чисел или чисел с плавающей запятой.
2. Понимайте значения числителя и знаменателя. Числитель - это количество частей, которые нужно взять, а знаменатель - это общее количество частей. Например, в дроби 2/5 две части нужно взять из пяти общих.
3. Сократите дробь. Если числитель и знаменатель имеют общие делители, их можно сократить путем деления на наибольший общий делитель. Например, дробь 6/8 можно сократить до 3/4, поскольку оба числа делятся на 2.
4. Выполняйте операции последовательно. При выполнении операций с дробями нужно последовательно выполнять сложение, вычитание, умножение и деление. Необходимо следить за порядком операций, чтобы избежать ошибок.
5. Используйте схемы или рисунки. В некоторых случаях может быть полезно использовать визуальные схемы или рисунки для лучшего понимания операций с дробями. Например, можно использовать круговые диаграммы для представления дробей.
6. Практикуйтесь. Чем больше вы практикуетесь в работе с дробями, тем более уверенным вы становитесь. Решайте математические задачи, выполняйте операции с дробями и проверяйте свои результаты. Это поможет вам закрепить материал и повысить навыки работы с дробями.
Следуя этим простым рекомендациям, вы сможете успешно освоить работу с дробями и достичь хороших результатов в этой теме математики.