Архитектура и математика неотделимы друг от друга. Точные расчеты, логика и пропорции являются неотъемлемой частью создания великолепных зданий. Профильная математика в архитектуре играет важную роль, позволяя архитекторам создавать устойчивые, функциональные и красивые сооружения.
Профильная математика применяется при проектировании зданий и определяет геометрическую форму, величину и пропорциональное соотношение его элементов. Это позволяет архитекторам создавать гармоничные и симметричные постройки, которые вызывают восторг у зрителей.
Примером применения профильной математики в архитектуре может служить знаменитая Буравская башня в Москве. Ее уникальная форма, напоминающая стрелу, была разработана с помощью математических расчетов. Архитекторы использовали понятие "золотого сечения", чтобы создать идеальное соотношение между шириной и высотой башни. Результатом стало захватывающее здание, которое стало символом современной архитектуры и превосходства человеческого интеллекта.
Влияние профильной математики на архитектуру

Профильная математика, с ее точностью и логикой, играет важную роль в архитектуре, помогая архитекторам разрабатывать инновационные и устойчивые дизайны зданий и сооружений. Применение математических концепций и алгоритмов позволяет архитекторам оптимизировать формы и структуры, учитывая как красоту, так и функциональность проекта.
Основная область применения профильной математики в архитектуре - это визуализация и моделирование. Архитекторы используют математические модели для создания трехмерных визуализаций и симуляций зданий, что позволяет им предложить клиенту лучшее представление о том, как будет выглядеть готовый проект.
Кроме того, профильная математика помогает архитекторам в анализе и проектировании структурных элементов зданий. Например, они могут использовать математические алгоритмы для определения оптимального распределения нагрузок и создания прочной и устойчивой конструкции.
| Примеры применения профильной математики в архитектуре: |
|---|
| 1. Фрактальные структуры: архитекторы могут использовать математические принципы фракталов для создания прекрасных и сложных форм зданий. |
| 2. Оптимизация энергоэффективности: математические модели помогают архитекторам находить оптимальные решения для минимизации затрат на энергию и повышения устойчивости зданий. |
| 3. Геометрические формы: профильная математика помогает архитекторам создавать уникальные геометрические формы, которые могут быть невозможны без математического анализа и моделирования. |
| 4. Расчеты систем вентиляции и освещения: математические модели позволяют архитекторам расчитывать оптимальные системы вентиляции и освещения, обеспечивая комфортные условия для жильцов. |
В целом, профильная математика дает архитекторам возможность создавать уникальные и функциональные проекты, удовлетворяющие как эстетическим критериям, так и требованиям эффективности и устойчивости. Без влияния математики архитектура не смогла бы достичь такого высокого уровня развития.
Важность применения профильной математики в архитектуре

Профильная математика играет ключевую роль в архитектуре, помогая архитекторам расставить пропорции, определить оптимальные размеры и форму зданий. Благодаря использованию математических принципов, проектирование становится эффективным и точным, что ведет к созданию устойчивых и эстетически привлекательных строений.
Одним из важных аспектов применения профильной математики в архитектуре является правильное использование пропорций. Пропорции определяются математически и опираются на золотое сечение, которое считается наиболее гармоничным для человеческого глаза. Архитекторы используют эти пропорции для создания симметричных и балансированных зданий, что придает им гармоничный и привлекательный вид.
Другим примером применения профильной математики в архитектуре является использование геометрических фигур. Архитекторы часто используют круги, квадраты, треугольники и другие геометрические формы для создания интересных и современных зданий. Точные математические расчеты позволяют им определить размеры и положение этих форм, что в конечном итоге создает уникальную архитектурную композицию.
Кроме того, профильная математика также играет важную роль в инженерных расчетах. Архитекторы используют математические модели и формулы для определения прочности и устойчивости конструкций, чтобы они могли выдерживать различные нагрузки, включая сильные ветры и землетрясения. Это позволяет создавать безопасные и надежные здания, способные противостоять экстремальным условиям.
В итоге, применение профильной математики в архитектуре является неотъемлемой частью проектирования и строительства зданий. Она помогает архитекторам достичь оптимальных результатов, создавая красивые и функциональные структуры. Поэтому профильная математика следует учитывать при всяком проектировании и строительстве, чтобы обеспечить высокое качество и долговечность зданий.
Примеры применения профильной математики в архитектуре

Профильная математика играет важную роль в архитектуре, помогая архитекторам создавать устойчивые и эстетически привлекательные сооружения. Вот несколько примеров, которые демонстрируют применение математических принципов в архитектуре:
Геометрические формы: Одним из проявлений профильной математики в архитектуре является использование геометрических форм. Архитекторы используют принципы геометрии для создания пропорций, углов и линий, которые обеспечивают гармоничный и сбалансированный внешний вид зданий.
Структурная стабильность: Профильная математика также применяется для обеспечения структурной стабильности зданий. Архитекторы используют математические расчеты для определения оптимальных пропорций и размеров стен, колонн, арок и других элементов конструкции здания. Это обеспечивает прочность и долговечность здания.
Освещение: Еще одним примером применения профильной математики в архитектуре является рассчеты освещения. Архитекторы используют математические модели для определения оптимального количества окон и их расположения, чтобы обеспечить достаточное естественное освещение внутри здания.
Аккустика: Математические расчеты также играют важную роль при проектировании зданий с хорошей акустикой. Архитекторы используют математические модели для определения оптимальной формы и материалов, которые будут обеспечивать равномерное распределение звука и минимизацию эха внутри здания.
Примеры применения профильной математики в архитектуре ярко демонстрируют не только важность математических навыков для успешной практики архитектора, но и их значимость для создания качественной и функциональной архитектуры, которая отвечает потребностям и предпочтениям людей.
Разработка архитектурных конструкций с использованием профильной математики

Профильная математика играет важную роль в разработке современных архитектурных конструкций, позволяя архитекторам создавать сложные формы и оптимизировать их структуру.
Одним из основных применений профильной математики в архитектуре является проектирование формы зданий. Архитекторы могут использовать геометрию и математические алгоритмы для создания уникальных и эстетически привлекательных форм, которые раньше были недоступны.
Кроме того, профильная математика может помочь в оптимизации структуры архитектурных конструкций. С помощью математических моделей и компьютерных алгоритмов, архитекторы могут рассчитывать оптимальное распределение нагрузок, повышая прочность и стабильность здания.
Профильная математика также играет важную роль в разработке фасадов и внутреннего оформления зданий. Архитекторы могут использовать математические алгоритмы для создания сложных и геометрически точных элементов фасадов, что позволяет достичь высокой визуальной привлекательности и оригинальности.
Некоторые известные примеры применения профильной математики в архитектуре включают здание Сиднейской оперы в Австралии, где геометрические принципы использовались для создания уникальной формы, а также Торсенсонский холл в Швеции, где математические модели были использованы для оптимизации структуры здания.
Ключевые принципы разработки архитектурных конструкций

1. Прочность и устойчивость. Архитектурные конструкции должны быть спроектированы с учетом распределения нагрузок и сил, чтобы обеспечить надежность и устойчивость сооружений. Например, при проектировании мостов или небоскребов необходимо учитывать ветровые нагрузки, взаимодействие материалов и гравитационную нагрузку.
2. Экономичность. Разработка архитектурных конструкций должна быть оптимизирована с точки зрения используемых материалов и затрат рабочей силы. Применение математических моделей позволяет определить оптимальные параметры и размеры конструкций, что снижает затраты на строительство и эксплуатацию.
3. Функциональность. Архитектурные конструкции должны соответствовать назначению сооружений и обеспечивать их функциональность. Например, при проектировании зданий необходимо учитывать расположение помещений, освещение, вентиляцию и необходимость размещения коммуникаций.
4. Эстетика. Разработка архитектурных конструкций должна учитывать эстетические аспекты и гармонично вписываться в окружающую среду. Профильная математика позволяет создавать гармоничные и пропорциональные формы, которые придают сооружениям уникальный и привлекательный вид.
Применение профильной математики в архитектуре играет важную роль в разработке архитектурных конструкций, помогая учитывать различные факторы и достигать оптимальных результатов. Вышеупомянутые принципы – всего лишь некоторые из основных, которые необходимо учесть при проектировании архитектуры.
Примеры архитектурных конструкций, основанных на профильной математике
- Статистические модели для прогнозирования нагрузки на конструкции: В архитектуре профильная математика используется для создания статистических моделей, прогнозирующих нагрузку на различные архитектурные элементы, такие как столбы, балки и стены. Это позволяет инженерам оптимизировать конструкции и обеспечить их долговечность и безопасность.
- Дизайн экологически эффективных зданий: Профильная математика применяется для разработки оптимальной формы здания, позволяющей снизить его потребление энергии и повысить энергетическую эффективность. Например, форма здания может быть оптимизирована с использованием профильной математики, чтобы максимально использовать естественное освещение и вентиляцию, что позволяет сократить использование искусственного освещения и кондиционирования воздуха.
- Формирование изящных архитектурных линий: Профильная математика используется для создания интригующих и эстетически привлекательных форм архитектурных элементов, таких как арки, куполы и фасады. Она позволяет архитекторам точно определить геометрические параметры исходного проекта и обеспечить его симметрию и гармонию.
- Оптимальное распределение нагрузок в высотных зданиях: Профильная математика играет важную роль в проектировании безопасных и устойчивых высотных зданий. Она позволяет определить оптимальное распределение нагрузок и статических сил в структурах здания, учитывая факторы, такие как ветеровоздействие и гравитацию. Такие здания, как небоскребы, требуют высокой степени технической точности и стабильности, которую обеспечивает профильная математика.
- Разработка запутанных и красочных фасадов: Профильная математика используется в архитектуре для создания запутанных и уникальных форм на фасадах зданий. Она позволяет создавать гладкие и изящные изгибы, перемещать и комбинировать различные геометрические фигуры, создавая впечатляющие фасады, которые становятся настоящими художественными произведениями.
Эти примеры демонстрируют важность профильной математики в архитектуре и ее влияние на создание выдающихся конструкций, которые сочетают в себе функциональность, эффективность и красоту.
Расчет прочности и надежности архитектурных элементов с помощью профильной математики
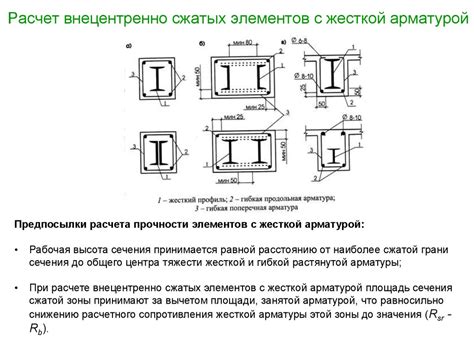
Профильная математика играет важную роль в расчете прочности и надежности архитектурных элементов. Это отрасль математики, которая изучает особенности форм, конструкций и материалов, используемых в архитектуре.
Одним из основных применений профильной математики является расчет прочности и надежности каркасов зданий, мостов и других строительных конструкций. С помощью различных алгоритмов и моделей профильная математика позволяет спрогнозировать, как конструкция будет себя вести при различных нагрузках и условиях эксплуатации.
Другим применением профильной математики является определение оптимальных размеров и формы элементов конструкции. Используя математические модели и вычисления, можно найти оптимальные значения параметров, которые обеспечивают максимальную прочность при минимальном расходе материалов.
Профильная математика также используется для анализа и проектирования фасадов зданий. С помощью математических моделей можно определить оптимальный профиль окна или элемента фасада, чтобы обеспечить наилучшее соотношение между эстетикой и энергосбережением.
Одним из примеров применения профильной математики в архитектуре является антивандальное остекление. С помощью математических моделей можно определить оптимальную форму стекла и его крепление, чтобы сделать его устойчивым к повреждениям и вандализму.
Таким образом, использование профильной математики в архитектуре позволяет повысить прочность, надежность и безопасность строительных конструкций, а также снизить затраты на материалы и энергопотребление.