Векторы в математике играют важную роль, так как они позволяют описывать и анализировать физические явления и процессы. Одной из характеристик векторов является их направленность. Векторы, которые имеют одно и то же направление, называются сонаправленными или коллинеарными.
Однако, не стоит путать эти два понятия. Векторы могут быть коллинеарными, но при этом иметь разные направления. Например, представьте себе два равных по длине отрезка, один направлен вдоль оси $x$, а другой - вдоль оси $y$. Эти два вектора будут коллинеарными, так как находятся на одной прямой, но направлены в разные стороны.
Сонаправленные векторы имеют не только одно и то же направление, но и совпадают по направлению. Другими словами, сонаправленные векторы идут в одну и ту же сторону. Это можно проиллюстрировать на примере двух векторов, описывающих движение двух автомобилей по одной дороге. Если оба автомобиля движутся в одну и ту же сторону, то их векторы будут сонаправленными.
Что такое векторы сонаправлены и коллинеарны

Векторы сонаправлены, когда они имеют одинаковое направление. Это означает, что они указывают в одну и ту же сторону. Другими словами, векторы сонаправлены, когда они лежат на одной прямой. Например, векторы, указывающие на север или восток, являются сонаправленными.
Векторы коллинеарны, когда они лежат на параллельных прямых. То есть, если все векторы принадлежат одной и той же прямой или их продолжения пересекаются в бесконечности, они называются коллинеарными. Например, два вектора, оба направленные вдоль оси x, или вектор, умноженный на скаляр, являются коллинеарными.
Векторы, которые сонаправлены и коллинеарны, обладают одинаковым направлением и могут быть представлены с использованием разных чисел или характеристик. Например, вектор (1, 2) и вектор (2, 4) являются сонаправленными и коллинеарными, так как у них одинаковое направление и отношение. Они лишь отличаются в размере.
Определение сонаправленных векторов

Два вектора считаются сонаправленными, если они совпадают по направлению и могут быть пропорционально измерены. Это означает, что сонаправленные векторы могут быть представлены как один и тот же вектор, умноженный на некоторую константу.
Можно представить пару сонаправленных векторов в виде прямой линии, где каждый вектор указывает на один и тот же конечный пункт, но может иметь разные длины.
| Примеры сонаправленных векторов: |
|---|
| 1. Векторы, которые указывают вдоль одной оси, например, векторы а = (2, 0) и b = (4, 0) сонаправлены вдоль оси x. |
| 2. Векторы, которые указывают в одну точку из разных начальных точек, например, векторы с = (1, 3) и d = (2, 4) сонаправлены к точке (3, 7). |
| 3. Векторы, которые имеют одинаковое направление, но различаются по длине, например, векторы e = (5, 0) и f = (10, 0) сонаправлены вдоль оси x и относятся друг к другу с коэффициентом 2. |
Понимание сонаправленных векторов является важным для изучения физики и математики, в частности векторов и геометрии. Знание о том, что два вектора сонаправлены, позволяет упростить множество вычислений и анализов, связанных с ними.
Определение коллинеарных векторов
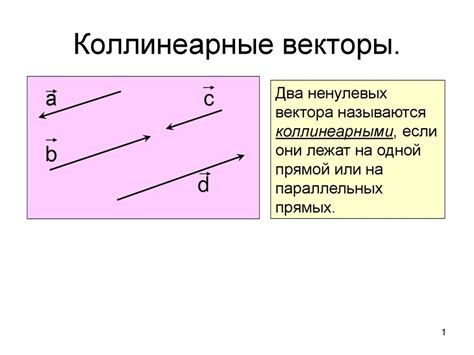
Два или более вектора называются коллинеарными, если они пропорциональны друг другу. Математически, векторы u и v считаются коллинеарными, если существует такое скалярное значение λ, которое умножается на один из них, чтобы получить другой:
u = λv
Здесь u и v – коллинеарные векторы, а λ – скаляр, называемый коэффициентом пропорциональности. Если скаляр λ положительный, то векторы сонаправлены, а если λ отрицательный, то векторы противоположно направлены.
Коллинеарные векторы имеют одинаковое направление и отличаются только по длине. Они лежат на одной прямой, могут быть параллельными или совпадающими. Например, векторы u(2, 3) и v(4, 6) являются коллинеарными, так как вектор v можно получить умножением вектора u на 2:
v = 2u = (2 * 2, 2 * 3) = (4, 6)
Отличия между векторами сонаправленными и коллинеарными
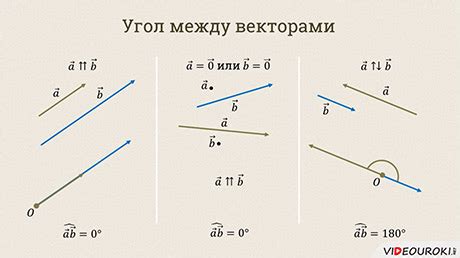
Векторы в математике играют важную роль и могут быть использованы для описания множества физических и геометрических явлений. Два таких понятия, как сонаправленность и коллинеарность, описывают отношение между векторами.
Сонаправленные векторы - это векторы, которые имеют одинаковое направление. Другими словами, они идут в одном и том же направлении. Векторы сонаправлены, когда они сонаправлены на оси координат или когда имеют одну и ту же ориентацию на пространственной диаграмме.
Коллинеарные векторы - это векторы, которые лежат на одной и той же прямой. Они могут иметь разную длину и могут быть направлены в разные стороны, но они все равно остаются коллинеарными, поскольку они находятся на одной и той же линии.
Таким образом, основное отличие между сонаправленными и коллинеарными векторами заключается в том, что сонаправленные векторы имеют одинаковое направление, в то время как коллинеарные векторы лежат на одной прямой.
Примерами сонаправленных векторов могут быть силы тяжести, которые действуют на тело вниз или вверх, или векторы скорости движения автомобилей по одному направлению.
Примером коллинеарных векторов могут быть векторы, которые описывают движение машины по прямой дороге, где один вектор представляет ее перемещение вперед, а другой вектор - перемещение назад в противоположном направлении.
Отличие в понятии

В математике и физике существует несколько понятий, связанных с векторами: "сонаправленность" и "коллинеарность". Эти понятия имеют некоторые сходства, но также отличаются по существу.
Когда говорят о сонаправленных векторах, подразумевают, что направления этих векторов совпадают. Сонаправленные векторы могут быть разной длины и иметь разную точку приложения, но их направления одинаковы.
С другой стороны, коллинеарные векторы - это векторы, которые лежат на одной прямой. Коллинеарные векторы имеют одинаковые или противоположные направления, но их точки приложения и длины могут быть разными.
Наглядным примером сонаправленных векторов могут служить стрелки, указывающие в одну сторону на изображении. Вектора сонаправленны друг другу, потому что их направления совпадают.
Примером коллинеарных векторов может быть натянутая на прямую резинка. Векторы, которые задают силу растяжения резинки, являются коллинеарными, так как они лежат на одной прямой, но их точки приложения и направления могут быть различными.
Отличие в геометрическом представлении

Отличие между сонаправленными и коллинеарными векторами можно увидеть в их геометрическом представлении.
Сонаправленные векторы представляют собой два (или более) вектора, которые направлены в одном и том же направлении на прямой линии. Такие векторы имеют одинаковую ориентацию и направление, но могут иметь разные длины. Например, векторы А(2, 1) и B(4, 2) являются сонаправленными, так как они направлены в одном и том же направлении.
С другой стороны, коллинеарные векторы представляют собой два (или более) вектора, которые лежат на одной прямой. Такие векторы могут иметь разные ориентации и направления, но должны иметь одинаковое отношение своих компонент. Например, векторы C(2, 1) и D(4, 2) являются коллинеарными, так как их компоненты относятся как 2:1.
Таким образом, отличие между сонаправленными и коллинеарными векторами заключается в их геометрическом представлении. Сонаправленные векторы лежат на одной прямой и имеют одинаковую ориентацию и направление, в то время как коллинеарные векторы могут иметь разные ориентации и направления, но лежат на одной прямой и имеют одинаковое отношение своих компонент.
Примеры сонаправленных и коллинеарных векторов
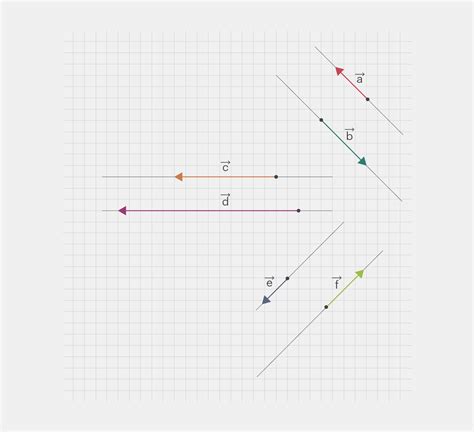
Приведем несколько примеров сонаправленных и коллинеарных векторов:
- Пример сонаправленных векторов:
- Векторы, указывающие на разные этажи в здании (например, векторы, указывающие на первый и второй этаж).
- Векторы, указывающие на движение автомобилей в одной полосе на дороге.
- Векторы, указывающие на движение лодок по одной реке.
- Векторы, указывающие на движение самолетов в одном направлении на небе.
- Векторы, имеющие одинаковый наклон на координатной оси.
- Векторы, параллельные друг другу и проходящие через одну точку.
- Векторы, имеющие одинаковое направление и пропорциональные длины.
- Векторы, указывающие на движение частиц в одной прямой линии.
Эти примеры демонстрируют связь между сонаправленными и коллинеарными векторами: сонаправленные векторы всегда являются коллинеарными, но коллинеарные векторы не всегда являются сонаправленными.