В мире математики существует множество различных объектов и понятий, которые помогают нам понять и описать окружающий нас мир. Одним из таких понятий является ребро. Ребро - это одна из основных составляющих элементов графа, который является абстрактной математической моделью представления связей между объектами.
В зависимости от контекста, ребра могут иметь различные разновидности и наименования. Одной из наиболее распространенных разновидностей ребер являются ориентированные ребра. Они обладают стрелкой, которая указывает направление связи между объектами графа. Такие ребра используются, например, в моделях дорожных сетей или в теории игр.
Другой разновидностью ребер являются взвешенные ребра. В этом случае, каждое ребро имеет свой вес или стоимость, которая отражает некоторую характеристику или значение связи между объектами графа. Такие ребра широко применяются в анализе данных, в задачах оптимизации и в транспортных моделях.
Кроме того, существуют еще множество других разновидностей ребер, таких как параллельные ребра, кратные ребра и др. Каждая из них имеет свои уникальные свойства и наименования, которые помогают нам лучше понять и описать связи между объектами в графе. Изучение различных разновидностей ребер является важной частью математической дисциплины и позволяет нам углубить свои знания о мире вокруг нас.
Разновидности ребер
Ребрами называются отрезки, которые соединяют вершины многоугольника. В зависимости от своего вида и положения относительно многоугольника, ребра могут быть различных типов.
1. Основные ребра
Основные ребра - это ребра, которые образуют границы многоугольника и определяют его форму. Они являются основными элементами, используемыми при описании многоугольника.
Пример:
В многоугольнике ABCDE семь основных ребер, образующих его границы: AB, BC, CD, DE, EA, AC и BD.
2. Диагонали
Диагонали - это ребра, которые соединяют две несоседние вершины многоугольника. Они не являются частью границы многоугольника и пересекают его внутренность.
Пример:
В многоугольнике ABCDE все возможные диагонали, соединяющие его вершины: AC, BD, AD, AE, BE и CE.
3. Боковые ребра
Боковыми ребрами называются ребра, которые соединяют соседние вершины многоугольника и лежат на его границе. Они образуют боковую поверхность многоугольника и помогают определить его объем и форму.
Пример:
В трехмерном многоугольнике ABCDEFG боковыми ребрами будут: AB, BC, CD, DE, EF, FG и GA.
Каждая разновидность ребра имеет свои особенности и связана с определенными характеристиками многоугольника.
Внешние ребра графа
Внешние ребра обычно носят дополнительные имена, которые отражают их специфическую роль в графе. К ним можно отнести следующие типы:
Входящие внешние ребра - это те ребра, которые соединяют вершины графа с вершинами, не входящими в него, но указывающие на входящий поток информации или ресурсов в граф.
Исходящие внешние ребра - это те ребра, которые соединяют вершины графа с вершинами, не входящими в него, но указывающие на исходящий поток информации или ресурсов из графа.
Периферийные внешние ребра - это те ребра, которые связывают вершины графа с внешними вершинами, не имеющими непосредственной связи с другими вершинами графа. Они играют важную роль в определении периферийной структуры графа.
Анализ внешних ребер графа позволяет понять, как взаимодействуют вершины графа с внешним окружением, а также выявить особенности его структуры и функционирования. Поэтому важно учитывать внешние ребра при анализе любой графовой модели.
Внутренние ребра графа
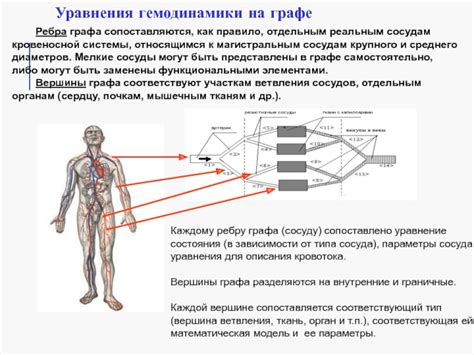
Они имеют свои особенности и различные причины их наименований. Например, внутренние ребра могут называться в соответствии с их ролями или функциями в графе.
- Ребра, соединяющие вершины разных компонентов связности, могут называться мостами или межкомпонентными ребрами.
- Ребра, которые необходимы для создания циклов в графе, могут называться циклическими ребрами или петлями.
- Ребра, которые соединяют вершины смежного слоя в дереве или графе, могут называться внутренними ребрами слоя.
- Ребра, соединяющие вершины, образующие замкнутый контур, могут называться границей или внутренними ребрами контура.
Таким образом, названия внутренних ребер графа могут отражать их роль или функцию в структуре графа и помогать лучше понять его особенности и свойства.
Ориентированные ребра графа
При работе с ориентированными графами некоторые ребра могут быть названы по определенным правилам, чтобы отразить направленность связи. Вот некоторые распространенные наименования ориентированных ребер:
- Входящее ребро - это ребро, которое входит в определенную вершину. Оно указывает на эту вершину из другой вершины графа.
- Исходящее ребро - это ребро, которое выходит из определенной вершины. Оно указывает на другую вершину графа из этой вершины.
- Переходное ребро - это ребро, которое связывает две вершины в разных компонентах графа. Оно указывает на вершину с меньшим индексом к вершине с большим индексом.
- Обратное ребро - это ребро, которое идет в обратном направлении по отношению к другому ребру. Оно указывает на вершину, которая ведет обратно к исходной вершине.
Ориентированные ребра могут быть использованы для моделирования различных явлений и процессов. Например, они могут использоваться для представления транспортных маршрутов, зависимостей между задачами в проекте или потока информации в сети.
Самопетли

Внешний вид самопетелей может быть разнообразным: они могут быть узкими и длинными, широкими и короткими, иметь сложную или простую форму. Их размеры также могут варьироваться, от нескольких миллиметров до нескольких сантиметров в длину.
Причины возникновения самопетлей до конца не изучены, но предполагается, что они могут быть связаны с генетическими факторами или влиянием окружающей среды во время развития эмбриона. Некоторые ученые также считают, что самопетли могут быть результатом мутаций или аномалий в развитии плода.
| Преимущества самопетелей | Недостатки самопетелей |
|---|---|
| Самопетли могут позволить ребру быть более гибким и подвижным, что положительно сказывается на адаптации организма к различным условиям. | Наличие самопетлей может быть связано со сниженной прочностью ребра и повышенной вероятностью повреждений. |
| Самопетли могут играть важную роль в процессе дыхания и обмена газами в организме. | Некоторые виды самопетлей могут вызывать дискомфорт и болевые ощущения у человека. |
| Изучение самопетлей может помочь ученым лучше понять процессы формирования и развития костной системы. | Самопетли могут быть признаком определенных заболеваний или патологий. |