Корень дискриминанта - это важное понятие в математике, которое используется для решения квадратных уравнений. Дискриминант позволяет определить, какое количество и какие типы корней имеет уравнение. Но как это вычислить быстро и просто?
Существует простая формула для нахождения корня дискриминанта. По определению, дискриминант равен разности квадрата коэффициента b и произведения коэффициентов a и c. То есть, D = b^2 - 4ac. Чтобы найти корень дискриминанта, достаточно взять квадратный корень от этой разности.
Чтобы вычислить корень дискриминанта быстро и без ошибок, можно воспользоваться специальными математическими программами или калькуляторами. В программе просто введите коэффициенты a, b и c, и вы получите результат. Калькуляторы с функцией корня дискриминанта также могут быть полезны, особенно при решении множества квадратных уравнений.
Но если вы хотите самостоятельно вычислить корень дискриминанта без помощи программы или калькулятора, то вам потребуется знать основы математики. Необходимые навыки включают умение работать с квадратными корнями, знание правил умножения и сложения, а также умение применять эти навыки к конкретным числам.
Как вычислить корень дискриминанта быстро и просто?

Формула для вычисления дискриминанта квадратного уравнения имеет вид:
D = b² - 4ac
где b, a и c - коэффициенты квадратного уравнения.
Для вычисления корня дискриминанта вам нужно:
- Возьмите значение дискриминанта (D).
- Подставьте это значение в формулу.
- Рассчитайте корень из полученного значения.
Корень дискриминанта позволяет определить, сколько корней имеет квадратное уравнение:
- Если дискриминант больше нуля и является полным квадратом, то у уравнения два различных действительных корня.
- Если дискриминант равен нулю, то у уравнения есть один действительный корень (корень совпадает).
- Если дискриминант меньше нуля, то у уравнения нет действительных корней (корни являются комплексными).
Теперь, зная, как вычислить корень дискриминанта быстро и просто, вы сможете решать квадратные уравнения более эффективно и точно.
Интуитивное понимание дискриминанта

Дискриминант вычисляется как разность квадрата коэффициента b и произведения коэффициента a на коэффициент c уравнения ax^2 + bx + c = 0. Для вычисления дискриминанта можно использовать формулу D = b^2 - 4ac.
Значение дискриминанта может быть положительным, отрицательным или равным нулю. Каждое из этих значений говорит нам о разном типе решений уравнения.
1. Если дискриминант больше нуля (D > 0), то у уравнения есть два разных корня. График будет пересекать ось X в двух точках.
2. Если дискриминант равен нулю (D = 0), то у уравнения есть один корень. График будет касаться оси X только в одной точке.
3. Если дискриминант меньше нуля (D < 0), то у уравнения нет действительных корней. График не будет пересекать ось X.
Таким образом, понимание значения дискриминанта помогает нам определить, сколько корней у квадратного уравнения и как они распределены на графике. Это важные знания, которые помогут нам решать квадратные уравнения и анализировать их графики.
Формула дискриминанта и ее значение
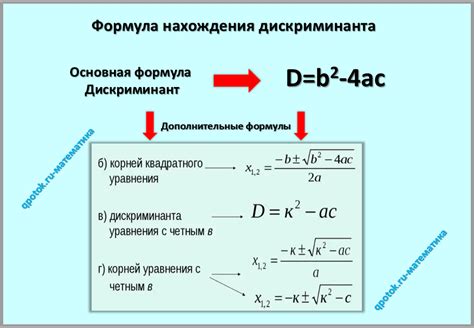
Д = b^2 - 4ac
Значение дискриминанта является ключевым показателем при решении квадратного уравнения. Оно позволяет определить, каким образом уравнение связано с его корнями.
1. Если дискриминант положительный (D > 0), то уравнение имеет два различных корня:
x1 = (-b + √D) / (2a)
x2 = (-b - √D) / (2a)
2. Если дискриминант равен нулю (D = 0), то уравнение имеет один корень:
x = -b / (2a)
3. Если дискриминант отрицательный (D < 0), то уравнение не имеет действительных корней, а имеет комплексные корни.
Знание формулы дискриминанта и его значения позволяет определить, какие корни имеет квадратное уравнение и как их вычислить.
Что означает положительный и отрицательный дискриминант?

Положительный дискриминант означает, что у квадратного уравнения есть два действительных корня. Это означает, что график функции пересекает ось абсцисс (горизонтальную ось) в двух точках. Физически это может означать, например, что у объекта есть два момента времени, когда его положение или скорость равны нулю.
Отрицательный дискриминант означает, что квадратное уравнение не имеет действительных корней. Это означает, что график функции не пересекает ось абсцисс. Физически это может означать, например, что у объекта нет момента времени, когда его положение или скорость равны нулю. Вместо этого уравнение имеет комплексные корни, которые являются мнимыми числами.
Зная знак дискриминанта, можно определить, сколько корней у квадратного уравнения и какие именно они могут быть. Это позволяет решать различные математические и физические задачи, связанные с квадратными уравнениями.
Что делать, если дискриминант равен нулю?

Если дискриминант равен нулю, то это означает, что квадратное уравнение имеет только один корень.
Чтобы найти этот корень, можно воспользоваться формулой корня квадратного уравнения:
x = -b / (2a), где a, b и c - коэффициенты уравнения ax^2 + bx + c = 0.
Или можно использовать другой метод - разложение на множители:
ax^2 + bx + c = a(x - x_1)(x - x_2), где x_1 и x_2 - корни уравнения.
Если дискриминант равен нулю, то уравнение может быть записано в виде:
ax^2 + bx + c = a(x - x_1)^2 = 0.
Отсюда следует, что единственный корень уравнения равен x_1, то есть x = x_1.
Таким образом, если дискриминант квадратного уравнения равен нулю, то уравнение имеет только один корень, который можно найти с помощью формулы корня или разложения на множители.
Как вычислить корень дискриминанта без формулы?

Вычисление корня дискриминанта может показаться сложной процедурой, особенно для тех, кто не имеет математического образования. Но на самом деле, существуют простые способы вычисления корня дискриминанта без использования формулы. В этом разделе мы рассмотрим несколько таких способов.
1. Использование таблицы квадратных корней. В таблице квадратных корней можно найти значения квадратных корней различных чисел. Для вычисления корня дискриминанта нужно найти значение квадратного корня ближайшего числа, которое меньше или равно дискриминанту. Например, для дискриминанта равного 9, можно использовать значение квадратного корня из 9, которое равно 3.
2. Использование приближенных значений. Можно использовать приближенные значения для вычисления корня дискриминанта. Например, для дискриминанта равного 16, приближенное значение корня можно взять равным 4.
3. Использование графического метода. Графический метод позволяет найти приближенное значение корня дискриминанта. Для этого можно построить график функции квадратного корня и найти точку пересечения графика с осью абсцисс, которая соответствует приближенному значению корня дискриминанта.
4. Использование онлайн калькуляторов. Существуют специальные онлайн калькуляторы, которые могут помочь вычислить корень дискриминанта. Вам нужно просто ввести значение дискриминанта и калькулятор автоматически найдет его корень.
Таким образом, вычисление корня дискриминанта без формулы может быть достаточно простым, если использовать таблицы, приближенные значения, графический метод или онлайн калькуляторы. Эти способы помогут вам быстро и эффективно вычислить корень дискриминанта и использовать его в нужных расчетах.
Примеры вычисления корня дискриминанта

Для вычисления корня дискриминанта используется формула:
Дискриминант = b^2 - 4ac
где a, b и c - коэффициенты квадратного уравнения ax^2 + bx + c = 0.
Давайте рассмотрим несколько примеров вычисления корня дискриминанта:
Пример 1:
Дано уравнение 2x^2 - 5x + 2 = 0:
a = 2, b = -5, c = 2
Дискриминант = (-5)^2 - 4 * 2 * 2 = 25 - 16 = 9
Корень дискриминанта = √9 = 3
Пример 2:
Дано уравнение x^2 + 6x + 9 = 0:
a = 1, b = 6, c = 9
Дискриминант = 6^2 - 4 * 1 * 9 = 36 - 36 = 0
Корень дискриминанта = √0 = 0
Пример 3:
Дано уравнение 3x^2 + 4x + 5 = 0:
a = 3, b = 4, c = 5
Дискриминант = 4^2 - 4 * 3 * 5 = 16 - 60 = -44
Дискриминант отрицательный, поэтому корень дискриминанта не существует.
Это были примеры вычисления корня дискриминанта. Надеюсь, что они помогли вам лучше понять эту тему.