Вычисление корня nной степени из числа является одной из важных задач в математике и ее приложениях. Нахождение корня nной степени позволяет нам извлекать квадратный корень и находить другие корни, такие как кубический, четвертный и т.д. Это особенно полезно при решении уравнений, анализе данных и в других областях, где требуется точное нахождение корней.
Существует несколько методов вычисления корня nной степени из числа. Один из наиболее распространенных методов - это метод Ньютона. Он основан на итерационном процессе и позволяет находить приближенное значение корня с заданной точностью. Другой метод - это метод возведения в степень. Он заключается в том, что мы возводим число в степень, обратную n, и полученное значение является корнем nной степени из исходного числа.
Рассмотрим примеры вычисления корня nной степени из числа. Предположим, что нам нужно найти корень квадратный из числа 16. С помощью метода возведения в степень мы получаем следующий результат: $\sqrt{16} = 16^{1/2} = 4$. То есть, квадратный корень из 16 равен 4. Используя метод Ньютона с начальным приближением x = 1, мы также получаем приближенное значение корня 4.
Что такое вычисление корня nной степени из числа

Вычисление корня nной степени из числа находит широкое применение в различных областях, включая математику, физику, инженерию и компьютерные науки. Оно используется для решения уравнений, приближенных вычислений, моделирования и анализа данных.
Существует несколько методов вычисления корня nной степени из числа, включая метод итераций, метод Ньютона и методы, основанные на разложении в ряд Тейлора. Каждый из этих методов имеет свои преимущества и ограничения.
Вычисление корня nной степени из числа может быть выполнено как с использованием вычислительных алгоритмов, так и с помощью специального программного обеспечения, встроенного в научные калькуляторы или математические пакеты.
Методы вычисления корня nной степени из числа

Метод деления отрезка пополам
Один из простых и эффективных методов вычисления корня nной степени из числа - это метод деления отрезка пополам. Он основан на принципе уточнения значения числа путем поиска его ближайшего корня.
Этот метод состоит в следующих шагах:
- Выбирается начальное приближение корня.
- Определяются два числа - левая и правая границы отрезка.
- Вычисляется среднее значение отрезка.
- Проверяется, лежит ли среднее значение в заданном допустимом диапазоне.
- Если значение лежит в допустимом диапазоне, то оно считается приближенным значением корня.
- Если значение не лежит в допустимом диапазоне, то определяется новый отрезок путем сужения выбранного отрезка.
- Шаги 3-6 повторяются до тех пор, пока значение не попадет в допустимый диапазон с заданной точностью.
Пример реализации:
def calculate_nth_root(number, n, precision):
low = 0
high = max(1, number)
middle = (low + high) / 2
while abs(number - middle ** n) > precision:
if middle ** n < number:
low = middle
else:
high = middle
middle = (low + high) / 2
return middle
Метод итераций
Еще один метод вычисления корня nной степени из числа - метод итераций. Он основан на итерационных вычислениях, когда текущее значение корня используется для получения следующего значения.
Этот метод состоит в следующих шагах:
- Выбирается начальное приближение корня.
- Применяется формула итерации для получения нового значения корня.
- Проверяется, выполняется ли условие прекращения итераций (заданная точность или достижение максимального числа итераций).
- Если условие прекращения не выполняется, то применяется новая итерация.
- Шаги 2-4 повторяются до достижения условия прекращения.
Пример реализации:
def calculate_nth_root(number, n, precision, max_iterations):
current_root = number / 2
for i in range(max_iterations):
next_root = ((n - 1) * current_root + number / current_root ** (n - 1)) / n
if abs(next_root - current_root) < precision:
break
current_root = next_root
return current_root
Это всего лишь два примера методов вычисления корня nной степени из числа. Существуют и другие подходы к решению этой задачи, каждый из которых имеет свои достоинства и недостатки. Выбор метода зависит от требуемой точности и производительности.
Метод простых итераций
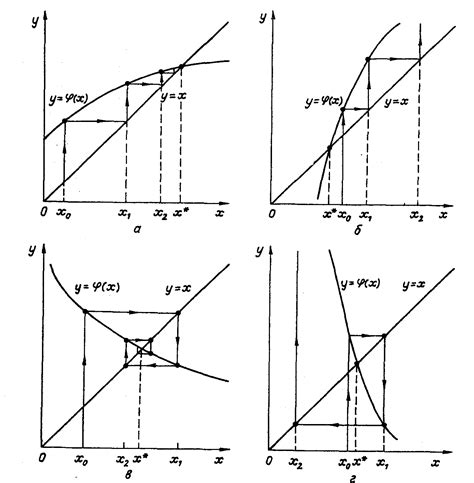
Пусть нам известно число a, из которого нужно извлечь корень n-ной степени. В методе простых итераций предлагается использовать итерационную формулу:
xi+1 = f(xi)
где f(x) - функция, заданная следующим образом:
f(x) = (1/n) * ((n-1) * x + a / x^(n-1))
Данная функция имеет неподвижную точку, которая соответствует корню уравнения. Таким образом, последовательность x1, x2, ..., xn будет приближаться к искомому корню с каждой итерацией.
Процесс вычисления корня n-ной степени методом простых итераций можно представить в виде таблицы:
| Шаг | xi | xi+1 |
|---|---|---|
| 1 | a/2 | f(a/2) |
| 2 | f(a/2) | f(f(a/2)) |
| 3 | f(f(a/2)) | f(f(f(a/2))) |
| ... | ... | ... |
Чем больше число итераций выполнено, тем ближе мы приближаемся к искомому корню. Критерием остановки может быть достижение заданной точности или достижение предельного числа итераций.
Метод простых итераций широко используется в математике, инженерии и других областях, где необходимо быстро и точно вычислить корень n-ной степени из числа.
Методы Ньютона
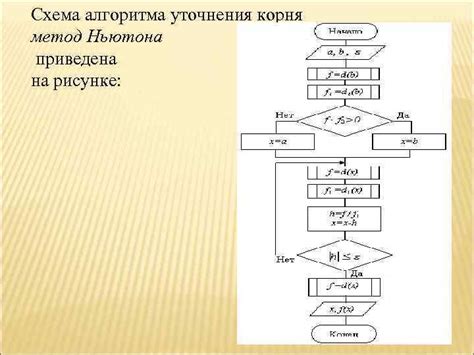
Одним из таких методов является метод Ньютона-Рафсона (или метод касательных). Он основан на теореме о среднем значении и использует линейную аппроксимацию функции вблизи предполагаемого корня. Этот метод сходится со скоростью квадратичной сходимости.
Алгоритм метода Ньютона-Рафсона для вычисления корня n-ной степени из числа выглядит следующим образом:
- Выбрать начальное приближение корня x0.
- Вычислить следующее приближение корня xk+1 по формуле: xk+1 = xk - f(xk)/f'(xk), где f(x) - функция, корнем которой является искомое число, а f'(x) - ее производная.
- Проверить условие окончания итерации. Если достигнута необходимая точность, т.е. |xk+1 - xk| < epsilon, где epsilon - заранее заданная малая величина, то остановить итерацию и принять xk+1 как приближенное значение корня.
- Иначе, принять полученное значение xk+1 как новое приближение корня и перейти к шагу 2.
Метод Ньютона-Рафсона часто применяется для решения уравнений, когда известна производная функции или ее можно вычислить. Однако, этот метод имеет некоторые ограничения, связанные с выбором начального приближения и наличием особых точек на графике функции.
В итоге, методы Ньютона предоставляют эффективный и быстрый способ нахождения корня n-ной степени из числа, но требуют некоторых предварительных вычислений и осторожного выбора начального приближения.
Примеры вычисления корня nной степени из числа

1. Метод итераций. Данный метод основан на последовательном приближении к искомому значению. Начиная с какого-либо начального приближения, осуществляется ряд итераций, в результате которых получается приближенное значение корня. Чем больше итераций, тем точнее будет полученный результат.
2. Метод Ньютона. Этот метод использует касательные к графику функции, что позволяет найти точное значение корня. Начиная с некоторого начального приближения, осуществляются последовательные итерации, в результате которых получается все более точное значение корня.
3. Метод деления отрезка пополам. Этот метод основан на разделении отрезка, на котором известно, что функция меняет знак, на две равные части. Затем анализируется, в какой половине отрезка находится корень, и процедура повторяется для выбранной половины. Итерации продолжаются до достижения требуемой точности.
Это лишь несколько примеров методов вычисления корня nной степени из числа. Используя различные алгоритмы, можно получить более точные результаты в зависимости от поставленной задачи.
Пример вычисления корня квадратного из числа

Один из простых методов вычисления корня квадратного - это метод приближений. Он заключается в последовательном уточнении приближенного значения корня. Начало алгоритма - это задание начального приближения. Затем мы используем формулу для уточнения приближенного значения, пока не достигнем нужной точности.
Пример:
Для вычисления корня квадратного из числа 16 применим метод приближений.
У нас есть начальное приближение: корень равен половине исходного числа: 16/2 = 8.
Уточнение приближения:
8^2 = 64, что больше исходного числа 16.
Делим 16 на текущее приближение и получаем новое приближение: 16/8 = 2.
Уточнение приближения:
2^2 = 4, что меньше исходного числа 16.
Делим 16 на текущее приближение и получаем новое приближение: 16/4 = 4.
Уточнение приближения:
4^2 = 16, что равно исходному числу 16. Процесс останавливается.
Искомый корень квадратный из числа 16 равен 4.
Таким образом, мы получили приближенное значение корня квадратного из числа 16 методом приближений. Этот метод может быть применен для вычисления корня квадратного из любого числа.
Пример вычисления корня кубического из числа

Для вычисления кубического корня из числа мы можем использовать методы бинарного поиска или метод Ньютона.
Рассмотрим пример вычисления кубического корня из числа 27.
Метод бинарного поиска:
Нам известно, что кубический корень из числа 27 равен 3, так как 3*3*3=27. Но давайте рассмотрим процесс бинарного поиска более формально.
Мы знаем, что кубический корень будет находиться в интервале от 0 до числа, для которого мы вычисляем корень. В нашем примере, это интервал от 0 до 27.
Мы начинаем с середины интервала, то есть с числа 13.5.
Сравниваем значение 13.5 в кубе с числом 27. Если оно больше, то новым интервалом становится интервал от 0 до 13.5. Если оно меньше или равно, то новым интервалом становится интервал от 13.5 до 27.
Далее продолжаем делить интервал пополам и сравнивать значения в кубе с числом 27 до тех пор, пока не найдем приближенное значение кубического корня. В нашем примере, это будет число 3.
Метод Ньютона:
Метод Ньютона основан на построении последовательности приближений к корню. Для вычисления кубического корня из числа 27 мы можем использовать следующую формулу:
xn+1 = xn - f(xn) / f'(xn),
где x0 - начальное приближение, f(x) - функция, корнем которой является число 27, f'(x) - производная этой функции.
Для нашего примера f(x) = x3 - 27, и производная f'(x) = 3x2.
Начальное приближение можно выбрать любое. Давайте выберем 3.
Применяем формулу и получаем следующее приближение: x1 = 3 - (33 - 27) / (3 * 3) = 2.3333.
Продолжаем применять формулу, пока не достигнем нужной точности. В нашем примере, после нескольких итераций, мы получим приближенное значение 3, что согласуется с точным значением.