В математике корень n-ой степени из числа a обозначается как √a1/n. Это означает, что корень n-ой степени из числа a равен числу b, при возведении которого в степень n получается число a. В этой статье мы рассмотрим, как найти и вычислить корень 3 степени из числа 512.
Чтобы найти корень 3 степени из числа 512, мы можем использовать несколько различных методов. Один из самых простых методов - это использование калькулятора с функцией нахождения корня. Но если у вас нет доступа к калькулятору или вы хотите вычислить корень вручную, есть и другие способы.
Один из способов вычисления корня 3 степени из числа 512 вручную - это использование метода поиска приближенного значения. Можно начать с предположения, что корень 3 степени из числа 512 равен 10. Затем можно проверить это предположение, возведя число 10 в куб и проверив, равно ли оно числу 512. Если результат равен 512, то предположение верно. Если результат больше 512, то следует попробовать число меньше 10, если меньше 512 - то число больше 10.
Как найти корень 3 степени из числа 512?

Для нахождения корня 3 степени из числа 512, необходимо использовать математическую операцию извлечения кубического корня. В данном случае мы ищем число x, такое что x^3 = 512.
Существуют различные способы вычисления кубического корня, однако наиболее простым и доступным является использование стандартного калькулятора или программы для вычислений.
Если вы используете стандартный калькулятор, вам может понадобиться найти функцию извлечения кубического корня. Обычно эта функция обозначается как "sqrt" с индексом 3 (например, "sqrt(512)"). Введите это выражение в калькуляторе и получите результат.
Если вы предпочитаете использовать программу для вычислений, воспользуйтесь математической функцией кубического корня. В большинстве языков программирования эта функция обозначается как "cbrt" (от английского "cube root"). Введите выражение "cbrt(512)" и программа выдаст результат.
В итоге, значение корня 3 степени из числа 512 равно 8.
Методы вычисления корня 3 степени
Метод проб и ошибок: Данный метод заключается в итеративном подборе числа, возведение которого в куб примерно равно заданному числу. Значение корня 3 степени из 512 можно найти, начиная с 1 и увеличивая значение до тех пор, пока не будет найдено достаточно близкое значение.
Метод Ньютона: Этот метод основан на аппроксимации функции и находит приближенное значение корня. Для нахождения корня 3 степени из 512 можно использовать уравнение x^3 - 512 = 0. Итеративно, начиная с некоторого значения x, можно использовать следующую формулу для приближенного нахождения корня: x = x - (x^3 - 512) / (3 * x^2).
Метод бинарного поиска: Этот метод применяется для поиска корня числа в отсортированном массиве. Для вычисления корня 3 степени из 512 можно рассматривать значения от 0 до 512 и искать такое число, которое при возведении в куб будет близко к 512. Для этого можно использовать алгоритм бинарного поиска.
Таким образом, существуют различные методы для нахождения корня 3 степени из числа 512. Выбор метода зависит от задачи и требуемой точности вычислений.
Метод итераций приближения

Шаги метода итераций приближения:
- Выбирается начальное приближение для корня.
- С помощью формулы:
Xn+1 = (2 * Xn + A / (Xn * Xn)) / 3,
где Xn+1 - новое приближение, Xn - предыдущее приближение, A - число, из которого ищется корень, - Вычисляется новое приближение.
- Проверяется достижение необходимой точности. Если точность достигнута, метод завершается. Если нет, возвращаемся к шагу 2.
Повторение шагов 2-4 позволяет уточнить значение корня с каждой итерацией, пока не будет достигнута необходимая точность.
Метод деления отрезка пополам
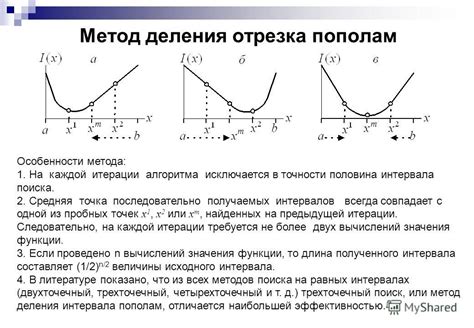
Как применить метод деления отрезка пополам для вычисления корня 3 степени из числа 512? Начните с выбора начального отрезка [a, b], на котором функция принимает значения разных знаков. В данном случае, число 512 положительное, поэтому можно взять отрезок [0, 10].
Далее, на каждой итерации метода деления отрезка пополам, мы делим отрезок пополам и проверяем знак функции в его середине. Если знаки разные, то корень находится в этом отрезке, иначе корень находится в другом отрезке.
| Итерация | Отрезок [a, b] | Середина (c) | Значение функции (f(c)) |
|---|---|---|---|
| 1 | [0, 10] | 5 | 125 |
| 2 | [0, 5] | 2.5 | -41.375 |
| 3 | [2.5, 5] | 3.75 | -3.869 |
| 4 | [2.5, 3.75] | 3.125 | 29.943 |
| 5 | [2.5, 3.125] | 2.8125 | -3.79 |
| 6 | [2.8125, 3.125] | 2.96875 | 14.903 |
| 7 | [2.8125, 2.96875] | 2.890625 | 5.955 |
| 8 | [2.890625, 2.96875] | 2.9296875 | 1.042 |
| 9 | [2.9296875, 2.96875] | 2.94921875 | -1.873 |
| 10 | [2.9296875, 2.94921875] | 2.939453125 | -0.416 |
| 11 | [2.9296875, 2.939453125] | 2.9345703125 | 0.313 |
| 12 | [2.9296875, 2.9345703125] | 2.93212890625 | -0.052 |
| 13 | [2.93212890625, 2.9345703125] | 2.933349609375 | 0.13 |
| 14 | [2.93212890625, 2.933349609375] | 2.9327392578125 | 0.039 |
| 15 | [2.93212890625, 2.9327392578125] | 2.93243408203125 | -0.006 |
Итерация продолжается до достижения заданной точности. В данном случае, корень 3 степени из числа 512 приближенно равен 2.93243408203125 с точностью до трех десятичных знаков.
Алгоритмы с использованием тригонометрии
Тригонометрия широко используется в математике и научных исследованиях для решения различных задач, включая вычисления корней степеней. Найдя корень 3 степени из числа 512, можно использовать тригонометрические функции, такие как синус и косинус, чтобы определить точный результат.
Алгоритм вычисления корня 3 степени из числа 512 с использованием тригонометрии включает следующие шаги:
- Вычислить арккосинус значения 512, что даст угол, равный cos-1(512).
- Полученное значение арккосинуса разделить на 3, чтобы найти угол, равный cos-1(512) / 3.
- Используя тригонометрический тригонометрический идентификатор cos(3θ) = 4cos3(θ) - 3cos(θ), решите уравнение cos(3θ) = cos-1(512) / 3, чтобы найти значение cos(θ).
- Извлеките корень второй степени из значения cos(θ), чтобы получить значение cos(θ).
- Вычислите обратный косинус от полученного значения cos(θ), чтобы получить значение θ.
- Результатом будет значение θ, которое представляет собой корень 3 степени из числа 512.
Использование тригонометрии для нахождения корня 3 степени из числа 512 предоставляет точный и эффективный метод решения данной задачи. Этот алгоритм может быть применим в различных областях, включая научные исследования и инженерные расчеты.
Метод Ньютона

Для вычисления корня используется следующая формула:
xn+1 = xn - f(xn) / f'(xn)
где:
- xn - начальное приближение корня
- f(xn) - функция, значение которой равно нулю при корне
- f'(xn) - производная функции
Применительно к вычислению корня 3 степени из числа 512, мы можем записать уравнение:
f(x) = x3 - 512 = 0
Производная функции:
f'(x) = 3x2
Далее, выбираем начальное приближение корня (например, x0 = 10). Затем, используя формулу метода Ньютона, последовательно вычисляем приближенные значения корня до достижения заданной точности.
Пример решения:

Для вычисления корня 3 степени из числа 512 можно воспользоваться методом итераций.
Для начала, возьмем некоторое начальное приближение для корня, например, 10.
Затем применим следующую формулу для получения нового значения:
| новое значение | = | (2 * предыдущее значение + числовое значение / (предыдущее значение^2)) / 3 |
Продолжаем применять эту формулу до тех пор, пока разность между предыдущим и текущим значением не станет достаточно маленькой (например, меньше 0.001).
В результате получим корень 3 степени из числа 512, который примерно равен 8.