Треугольник - одна из основных фигур в геометрии, и вычисление его корня является важной задачей при решении различных проблем. Корень треугольника определяет его центр, который может быть использован для решения задач, связанных с площадью, периметром, а также построением окружностей, вписанных и описанных вокруг треугольника.
Существует несколько методов для вычисления корня треугольника. Один из самых простых и часто используемых методов - метод центра тяжести. Согласно этому методу, корень треугольника находится в точке пересечения медиан - линий, соединяющих вершины треугольника с серединами противоположных сторон. Метод центра тяжести основан на том, что массы трех медиан равны, и способность этих медиан пересекаться в одной точке.
Другой метод для вычисления корня треугольника - метод инсцентра. Он основан на концепции точки, в которой вписанная окружность треугольника касается каждой стороны треугольника. Точка, где эти три линии сходятся, является корнем треугольника. В отличие от метода центра тяжести, метод инсцентра требует геометрического построения окружностей и проведения трех линий, что может быть достаточно сложным в некоторых случаях.
Основные методы вычисления корня треугольника
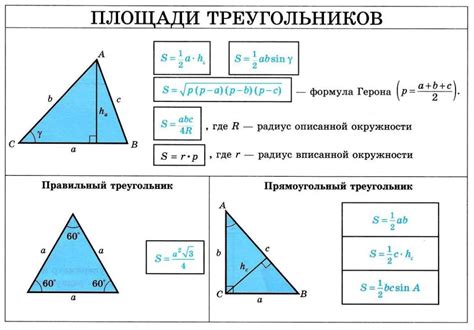
1. Метод Герона
Метод Герона является одним из самых известных и широко используемых методов для вычисления корня треугольника. Он основан на итерационном процессе, который позволяет приближенно определить корень с заданной точностью. Метод Герона основан на использовании формулы:
xn+1 = (xn + a/xn)/2
где xn+1 - новое приближение корня, xn - предыдущее приближение корня, a - значение, для которого вычисляется корень. Метод Герона применяется для нахождения длины стороны треугольника, площади треугольника и других геометрических характеристик.
2. Метод трех косинусов
Метод трех косинусов основан на использовании теоремы косинусов для вычисления длин сторон треугольника. Согласно этому методу, длины сторон треугольника могут быть определены с использованием углов треугольника и известной стороны. Формула для определения длины стороны треугольника с использованием метода трех косинусов выглядит следующим образом:
a2 = b2 + c2 - 2bc * cos(A)
где a - длина стороны треугольника, b и c - длины других сторон треугольника, A - угол между стороной b и стороной c. Метод трех косинусов используется для вычисления неизвестной стороны треугольника при известных углах и других сторонах.
3. Метод синусов
Метод синусов основан на использовании теоремы синусов для вычисления длин сторон треугольника. Согласно этому методу, длины сторон треугольника могут быть определены с использованием известных углов треугольника и соответствующих сторон. Формула для определения длины стороны треугольника с использованием метода синусов выглядит следующим образом:
a/sin(A) = b/sin(B) = c/sin(C)
где a, b и c - длины сторон треугольника, A, B и C - соответствующие углы треугольника. Метод синусов используется для определения длины неизвестной стороны треугольника при известных углах и других сторонах.
Это лишь некоторые из основных методов вычисления корня треугольника. В зависимости от конкретной задачи и доступных данных, можно выбрать подходящий метод для решения поставленной задачи.
Метод Герона: эффективное решение задачи
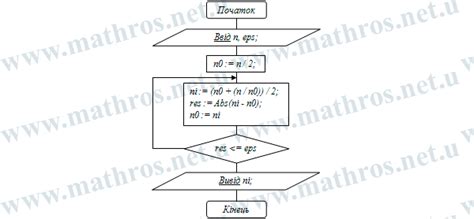
Для решения задачи методом Герона необходимо знать длины всех сторон треугольника. Процесс вычисления корня начинается с задания начального приближения. Чаще всего в качестве начального значения используется половина суммы длин сторон треугольника.
Затем выполняется итерация: на каждом шаге находится среднее арифметическое между предыдущим значением и результатом деления площади треугольника на половину средней линии, то есть на половину длины стороны, полученной на предыдущем шаге.
Процесс итерации продолжается до достижения необходимой точности. Точность может быть определена заранее или же зависеть от величины погрешности вычислений.
Метод Герона является эффективным решением задачи вычисления корня треугольника. Он позволяет получить приближенное значение корня с заданной точностью за конечное количество итераций. Однако при выборе начального приближения следует быть внимательным, чтобы избежать сходимости к бесконечности или неправильному решению.
Важно понимать, что метод Герона является численным методом и не всегда дает точное значение корня треугольника. Поэтому результаты следует проверять и округлять до необходимой точности.
Метод половинного деления: простота и точность

Суть метода состоит в последовательном делении интервала на две равные части и определении, на какой половине отрезка находится корень. Затем процесс продолжается в выбранной половине, и так далее, пока не будет достигнута требуемая точность. Этот метод обладает высокой точностью в результате многократного деления и относительно небольшими затратами вычислительных ресурсов.
Метод половинного деления находит широкое применение для решения различных задач, в том числе и в вычислениях геометрических параметров треугольника. При помощи этого метода можно эффективно вычислять площадь треугольника, длину его сторон, углы и радиусы вписанных и описанных окружностей.
Однако необходимо учитывать, что метод половинного деления требует предварительного выбора начального приближения и определенной сходимости функции на заданном отрезке. В противном случае может возникнуть риск ошибочных результатов или необходимости повторных вычислений.
Метод итераций: поиск корня с помощью последовательных приближений
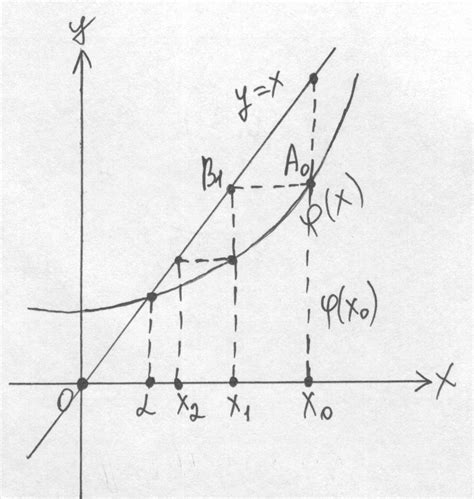
Основная идея метода итераций заключается в следующем:
- Выбрать начальное приближение корня функции.
- Вычислить значение функции в выбранной точке.
- Сдвинуть приближение корня в направлении уменьшения значения функции.
- Повторять шаги 2 и 3 до достижения нужной точности или конечной точки.
Важно отметить, что метод итераций может сходиться к решению только при определенных условиях, например, при наличии неподвижной точки. Поэтому правильный выбор начального приближения и функции итерации является ключевым для эффективной работы метода.
Преимущества метода итераций:
- Простота реализации и понимания.
- Возможность использования для различных типов функций.
- Получение приближенного решения с заданной точностью.
Недостатки метода итераций:
- Сходимость метода не всегда гарантирована.
- Скорость сходимости может быть низкой.
- Сложность выбора начального приближения и функции итерации.
В целом, метод итераций является одним из важных инструментов для нахождения корней функций. Он может быть использован как самостоятельный метод, так и в комбинации с другими численными методами для повышения эффективности.
Метод Ньютона: быстрое сходимое к точному значению
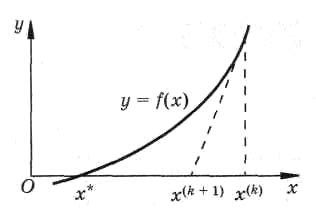
Идея метода Ньютона состоит в последовательном приближении к корню путем использования касательных кривых. Алгоритм начинает с некоторого начального приближения и далее находит уточненное значение корня путем нахождения точки пересечения касательной с осью абсцисс. Этот процесс повторяется до достижения заданной точности.
Для применения метода Ньютона к вычислению корня треугольника, сначала необходимо выбрать начальное приближение, например, среднюю точку основания треугольника. Затем выполняется итерационный процесс, на каждом шаге которого находится уточненное значение корня с использованием формулы:
xn+1 = xn - f(xn)/f'(xn)
где xn - текущее приближение, f(xn) - значение функции в точке xn, и f'(xn) - значение производной функции в точке xn. Это уточненное значение используется как новое приближение на следующем шаге.
Метод Ньютона сходится к корню треугольника с квадратичной скоростью, что означает, что с каждой итерацией погрешность сокращается в квадрате. Это делает его очень эффективным в сравнении с другими методами.
Однако, стоит отметить, что метод Ньютона требует знания функции и ее производной, что может быть сложным в случае сложных и нелинейных функций. Также при неправильном выборе начального приближения метод может не сойтись к корню или сойтись к неверному значению.
Метод бисекции: область изоляции корня и его нахождение
Одним из важных этапов использования метода бисекции является выбор области изоляции корня. Область изоляции определяется двумя начальными точками: левым концом отрезка и правым концом отрезка. Принципиальное условие этого выбора - наличие корня на отрезке, по которому будет проводиться деление.
В начале работы метода бисекции определяются значения функции в левой и правой границе отрезка. Затем знаки этих значений сравниваются. Если знаки разные, это означает, что на данном отрезке содержится корень треугольника. Если знаки одинаковые, отрезок делится пополам и в середине отрезка определяется значение функции. Затем снова выполняется сравнение знаков и процесс деления повторяется до тех пор, пока не будет достигнута заданная точность или не будет найден корень.
Метод бисекции позволяет получить достаточно точный результат при нахождении корня треугольника, особенно в случаях, когда начальная область изоляции корня широкая. Однако при применении этого метода необходимо учитывать, что он требует большего числа итераций по сравнению с некоторыми другими методами. Поэтому, для достижения большей эффективности при решении задачи нахождения корня треугольника, рекомендуется использование других методов, таких как метод Ньютона или метод секущих.
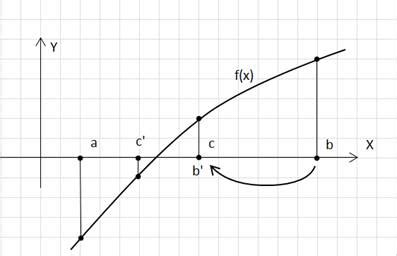
Метод Хорд: альтернативный подход к вычислению корня
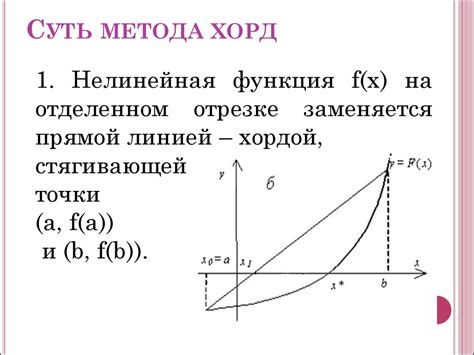
При использовании метода Хорд находится прямая, соединяющая две точки графика функции, и затем рассчитывается точка пересечения этой прямой с осью абсцисс. Затем процесс повторяется, причем каждый раз вычисляется новая прямая, ищущая пересечение с осью абсцисс. Таким образом, метод Хорд последовательно приближается к корню функции с каждым шагом.
Для более точных результатов, метод Хорд требует знания начального приближения корня функции. Также для его применения необходимо знание уравнения функции и ее графика. Поэтому для сложных функций этот метод может быть неэффективным.
Однако метод Хорд применяется с успехом во многих простых и средне-сложных задачах. Он является альтернативой другим методам, таким как метод бисекции или метод Ньютона, и может быть полезным в случаях, когда эти методы неэффективны или неприменимы.
Важно отметить, что метод Хорд не является гарантией полного нахождения корня функции. В зависимости от выбранного начального приближения и формы функции, метод Хорд может сходиться к некоторому приближению корня или расходиться, не достигнув конечного результата.
Тем не менее, метод Хорд остается важным инструментом в арсенале методов для вычисления корней треугольника. Он предлагает альтернативный подход, который может быть полезным в определенных ситуациях и позволяет получить приближенные значения корня функции.