</p>
Окружность – это геометрическая фигура, представляющая собой множество точек, равноудаленных от центра. На практике окружности часто встречаются в различных областях знания и используются для решения разнообразных задач. Одним из важных параметров окружности является её объем, который позволяет определить, сколько материала необходимо для создания объемного объекта с окружностью в качестве основания.
Формула для вычисления объема окружности зависит от её размеров и может быть представлена в различных вариантах. В общем случае, для нахождения объема окружности используется следующая формула: V = (4/3) × π × r³, где V – объем, π – число π (приближенное значение равно 3.14), r – радиус окружности.
Существует несколько способов вычисления объема окружности. Один из них основан на использовании значения диаметра окружности, а другой – на радиусе. В обоих случаях необходимо знать соответствующие формулы и подставить в них известные значения. Исходя из полученного результата, можно принять решение о количестве требуемого материала для создания конкретного объемного объекта на основе окружности.
Что такое объем окружности и как его найти

Для того, чтобы найти объем окружности, мы можем использовать формулу для объема шара, так как окружность является плоским сечением шара. Формула для объема шара: V = (4/3) * π * r^3, где V - объем, π - число Пи (приближенное значение составляет около 3.14159), r - радиус окружности.
Если мы знаем радиус окружности, мы можем подставить его в формулу и вычислить объем окружности. Результатом будет значение, выраженное в кубических единицах, так как объем измеряется в трехмерном пространстве.
Нахождение объема окружности может быть полезно в различных областях, таких как геометрия, физика, инженерное дело и архитектура. Зная объем окружности, можно производить различные расчеты и прогнозы, связанные с пространственными параметрами объектов.
Формула для вычисления объема окружности
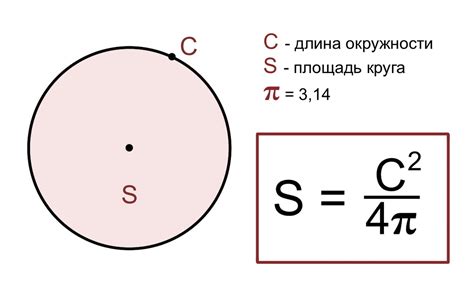
Для вычисления объема окружности необходимо знать ее радиус. Объем окружности можно вычислить по формуле:
V = (4/3) * π * r^3
Где V - объем окружности, π - число пи (приблизительно равное 3.14), r - радиус окружности.
Для использования данной формулы достаточно знать значение радиуса окружности. Просто введите значение радиуса в формулу и выполните необходимые вычисления. Полученное число будет являться объемом окружности.
Способы вычисления объема окружности
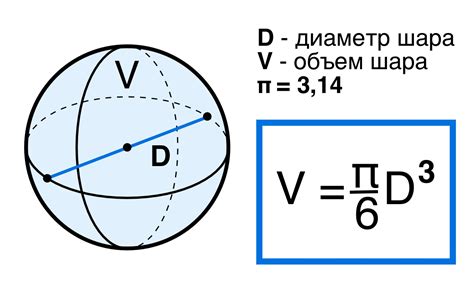
Существует несколько способов вычисления объема окружности, в зависимости от доступных данных и поставленной задачи.
| Метод | Формула |
|---|---|
| Метод цилиндра | V = πr^2h |
| Метод шара | V = (4/3)πr^3 |
Метод цилиндра основан на представлении окружности как боковой поверхности цилиндра, а метод шара основан на представлении окружности как поверхности шара.
Для использования этих формул необходимо знать радиус окружности (r) и высоту цилиндра (h) или радиус шара (r).
Обратите внимание, что значением числа π можно принять 3.14 или использовать более точное значение 3.14159, в зависимости от необходимой точности вычислений.
Выбор метода вычисления объема окружности зависит от контекста задачи и требуемой точности результатов. Важно учитывать также единицы измерения, в которых представлены данные, и приводить результаты к соответствующим единицам.