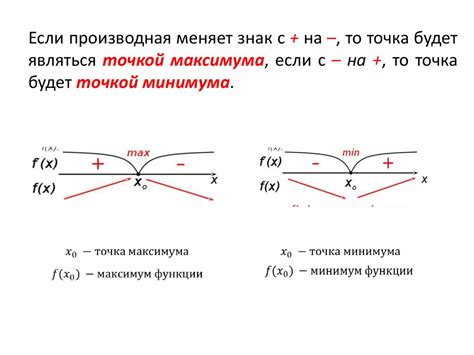
Вычисление производной является одной из основных операций математического анализа. Она позволяет определить скорость изменения функции в заданной точке. Но что если мы захотим вычислить производную не функции, а цифры? Что это означает и как это делается?
Вычисление производной цифры может показаться странным и непонятным на первый взгляд, но на самом деле это очень интересный математический подход. В основе этого подхода лежит идея представления цифры в виде функции, которая зависит от положения этой цифры в числе.
Например, рассмотрим цифру 5. Мы можем представить ее в виде функции f(x), где x - положение этой цифры в числе. Тогда мы можем задать вопрос: как скорость изменения цифры 5 зависит от ее положения в числе?
Что такое производная цифры и почему она важна?

Производная цифры представляет собой понятие из области математики, которое определяет, как изменяется значение цифры при изменении ее позиции в числе. Более конкретно, производная цифры показывает, насколько быстро значение цифры меняется по отношению к изменению ее позиции.
Понимание производной цифры является важным для решения множества задач, связанных с числами и их изменениями. В частности, производная цифры широко применяется в финансовых расчетах, физических моделях, статистике и программировании.
Знание производной цифры позволяет анализировать и предсказывать изменения значений цифр в числах. Оно помогает определить экстремальные значения, моменты перелома, скорости изменений и другие характеристики, критически важные для принятия решений в различных областях деятельности.
Важно отметить, что производная цифры может быть положительной, отрицательной или равной нулю, в зависимости от того, как значение цифры меняется при изменении ее позиции. Эта информация помогает аналитикам и исследователям лучше понять и интерпретировать данные и результаты их исследований.
Таким образом, знание и понимание производной цифры является необходимым инструментом для тех, кто работает с числами и их анализом. Оно позволяет более точно и эффективно решать задачи, связанные с изменениями значений цифр, и способствует принятию обоснованных решений в различных областях деятельности.
Применение производной цифры
Одной из областей, где применение производной цифры находит широкое применение, является математический анализ. Здесь производная цифры используется для нахождения скорости изменения функции в зависимости от аргумента.
Также производная цифры может быть полезной в физике. Например, при изучении движения тела в пространстве производная цифры используется для определения скорости и ускорения тела.
В биологии производная цифры помогает в анализе изменения популяции организмов в зависимости от времени. Она позволяет определить, изменяется ли популяция организмов с постоянной скоростью или есть другие факторы, влияющие на ее изменение.
Применение производной цифры также находит в экономике. Она позволяет анализировать изменение различных экономических показателей, таких как прибыль, спрос, предложение и т. д.
Наконец, производная цифры используется и в информатике. Она позволяет определить скорость выполнения алгоритма и влияние различных факторов на производительность программы.
Таким образом, применение производной цифры охватывает широкий спектр научных и практических областей и является неотъемлемой частью математического анализа и других наук. Она позволяет анализировать изменение величин и оптимизировать различные процессы.
Алгоритм вычисления производной цифры

Для вычисления производной цифры в заданном числе можно использовать следующий алгоритм:
- Разложить число на отдельные цифры.
- Выбрать цифру, относительно которой вычисляется производная.
- Умножить выбранную цифру на ее порядковый номер начиная с 1.
- Вычесть из полученного произведения сумму номеров всех цифр числа.
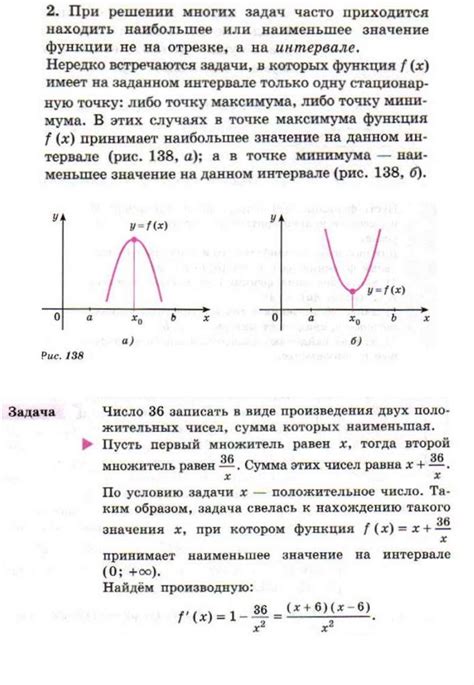
Таким образом, алгоритм позволяет получить результат - производную цифры в заданном числе. Этот метод может использоваться для анализа различных числовых последовательностей, а также для решения задач математического анализа.
Примеры использования производной цифры
Производная цифры может быть полезной в различных областях. Рассмотрим несколько примеров:
| Пример | Описание |
|---|---|
| 1. Финансовая аналитика | При анализе финансовых данных, производная цифры может использоваться для выявления изменений в динамике доходов и расходов. Например, изменение производной цифры может указывать на снижение или увеличение доходности компании. |
| 2. Машинное обучение | В задачах классификации и регрессии, использование производной цифры может быть одним из способов извлечения признаков из данных. Например, производная цифры может помочь выявить изменения в траектории движения объекта на видеозаписи. |
| 3. Анализ временных рядов | Для прогнозирования и анализа временных рядов, производная цифры может использоваться для выявления трендов и сезонности. Например, изменение производной цифры может указывать на начало или конец сезонного изменения данных. |
| 4. Криптография | В криптографии, производная цифры может использоваться для генерации случайных чисел или создания хэш-функций. Например, производная цифры может служить основой для определения ключей шифрования. |