Одним из важных аспектов в электротехнике является вычисление общего сопротивления в параллельном соединении электрических элементов. Параллельное соединение представляет собой ситуацию, при которой различные элементы подключены параллельно друг другу. В таких случаях сопротивления элементов складываются с помощью определенных методов, что позволяет получить итоговое сопротивление электрической цепи.
Один из наиболее распространенных методов вычисления сопротивления в параллельном соединении - это формула обратного значения. Согласно этой формуле, сопротивления каждого элемента инвертируются (т.е. заменяются на их обратные значения), после чего их суммируют и получают общее сопротивление цепи. Для более наглядного представления формула может выглядеть следующим образом:
1/Rобщ = 1/R1 + 1/R2 + ... + 1/Rn
Однако, помимо этого метода, существует и другой способ расчета общего сопротивления в параллельном соединении - использование эффективного сопротивления. Этот метод заключается в нахождении обратного значения для каждой нити цепи, после чего сопротивления складываются и находят их обратное значение. Таким образом, формула для вычисления сопротивления в параллельном соединении с использованием эффективного сопротивления может быть записана следующим образом:
Rобщ = 1 / (1/R1 + 1/R2 + ... + 1/Rn)
Чтобы лучше понять данный материал, рассмотрим пример. Допустим, у нас есть два резистора параллельно соединенных в электрической цепи. Первый резистор имеет значение 3 Ом, а второй - 2 Ом. Тогда применяя формулу обратного значения, мы можем вычислить итоговое сопротивление:
1/Rобщ = 1/3 + 1/2 = 5/6
Rобщ = 6/5 ≈ 1.2 Ом.
Таким образом, общее сопротивление параллельного соединения резисторов составляет примерно 1.2 Ом. Знание методик вычисления сопротивления в параллельном соединении помогает электротехникам эффективно планировать и строить электрические цепи для различных приложений.
Что такое параллельное соединение
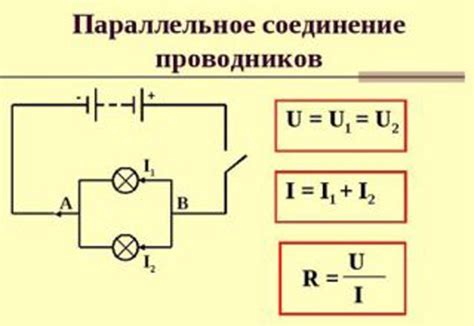
Параллельное соединение обладает рядом особенностей. Во-первых, в таком соединении суммарное сопротивление цепи уменьшается по сравнению с сопротивлением каждого отдельного элемента. То есть, если в цепи есть несколько резисторов, соединенных параллельно, то суммарное сопротивление будет меньше, чем наименьшее из них.
Во-вторых, ток, проходящий через параллельно соединенные элементы, делится между ними пропорционально их сопротивлениям. Это означает, что если в цепи есть два резистора, сопротивление первого из которых в два раза больше, чем у второго, то ток, проходящий через первый резистор, будет в два раза меньше тока, проходящего через второй резистор.
Параллельное соединение широко применяется в электрических схемах, так как позволяет эффективно управлять током и сопротивлением в цепи. При проектировании электрических устройств необходимо учитывать особенности параллельного соединения для достижения желаемых характеристик и оптимальной работы системы.
Методы вычисления сопротивления в параллельном соединении

Один из методов вычисления сопротивления в параллельном соединении - использование обратного значения общего сопротивления, равного сумме обратных значений сопротивлений элементов. То есть, если имеется несколько сопротивлений R1, R2, R3 в параллельном соединении, то общее сопротивление Rp может быть вычислено по формуле:
Rp = 1 / (1/R1 + 1/R2 + 1/R3)
Другой метод вычисления общего сопротивления - использование отношения между общим сопротивлением и средним значениям сопротивлений элементов. В этом случае формула для вычисления общего сопротивления будет иметь вид:
Rp = (R1 * R2 * R3) / (R1 + R2 + R3)
Также существует метод расчета общего сопротивления с использованием таблиц. При этом каждое сопротивление помещается в отдельную ячейку таблицы, а результат вычисления общего сопротивления помещается в отдельную ячейку в той же строке. Таким образом, получается таблица, в которой столбцы соответствуют сопротивлениям, а строка с результатом вычисления общего сопротивления. Этот метод более удобен при работе с большим количеством сопротивлений.
| Сопротивление 1 | Сопротивление 2 | Сопротивление 3 | Общее сопротивление |
|---|---|---|---|
| R1 | R2 | R3 | Rp |
Вычисление сопротивления в параллельном соединении является неотъемлемой частью работы в области электроники и электрических цепей. Знание различных методов вычисления позволяет эффективно проектировать и анализировать параллельные цепи.
Метод общего сопротивления
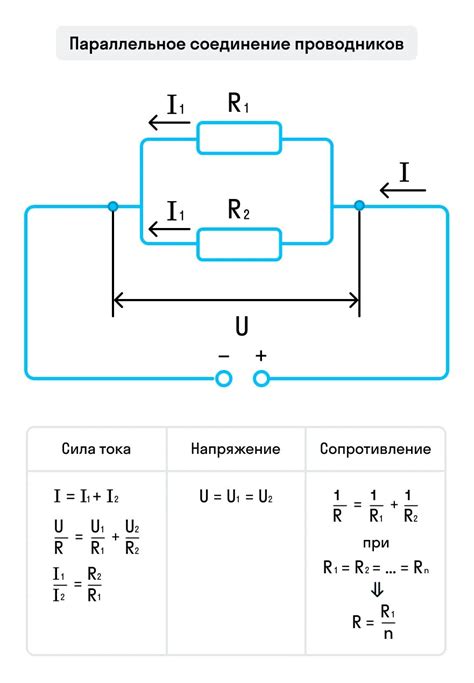
Для применения метода общего сопротивления необходимо знать сопротивления всех элементов, которые соединяются параллельно, их количество и номиналы. Далее выполняются следующие шаги:
- Найти обратные величины всех сопротивлений. Для этого каждое сопротивление нужно разделить на единицу.
- Сложить все обратные величины сопротивлений.
- Найти обратную величину полученной суммы.
- Полученную обратную величину нужно разделить на единицу, чтобы найти эквивалентное сопротивление.
Например, если имеется два сопротивления R1 = 4 Ом и R2 = 6 Ом, то применяя метод общего сопротивления, можно вычислить эквивалентное сопротивление:
- Найдем обратные величины сопротивлений: 1/R1 = 1/4 Ом и 1/R2 = 1/6 Ом.
- Сложим обратные величины: 1/R1 + 1/R2 = 1/4 Ом + 1/6 Ом = 3/12 Ом + 2/12 Ом = 5/12 Ом.
- Найдем обратную величину полученной суммы: 1/(1/R1 + 1/R2) = 1/(5/12 Ом) = 12/5 Ом.
- Разделим полученную обратную величину на единицу: 1/(12/5 Ом) = 5/12 Ом.
Таким образом, эквивалентное сопротивление для данного примера будет равно 5/12 Ом.
Использование метода общего сопротивления позволяет упростить вычисления в параллельных соединениях, особенно когда имеется большое количество сопротивлений. Он также позволяет учесть все значения сопротивлений и получить точный результат.
Метод обратных величин

Rпар = 1 / (1/R1 + 1/R2 + 1/R3 + ... + 1/Rn)
где Rпар - сопротивление параллельного соединения, R1, R2, R3, ..., Rn - сопротивления элементов, соединенных параллельно.
Чтобы применить метод обратных величин к конкретной задаче, необходимо знать значения всех сопротивлений в параллельном соединении. Затем используя формулу, производится вычисление обратных величин для каждого элемента, после чего все результаты суммируются и обратное значение от полученной суммы является искомым сопротивлением параллельного соединения.
Этот метод позволяет обрабатывать различные комбинации параллельных сопротивлений и находить общее их сопротивление. Необходимо только помнить, что в случае, если одно из сопротивлений стремится к нулю, общее сопротивление будет равно нулю.
Примеры вычисления сопротивления в параллельном соединении
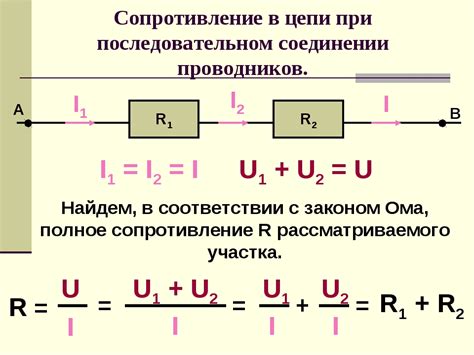
В параллельном соединении сопротивления складываются по формуле:
1/Рпараллельное = 1/Р1 + 1/Р2 + 1/Р3 + ... + 1/Рn
Где Рпараллельное - сопротивление в параллельном соединении, Р1, Р2, Р3 и так далее - значения сопротивлений, соединенных параллельно.
Рассмотрим несколько примеров вычисления сопротивления в параллельном соединении:
- Пример 1: В параллельное соединение подключены резисторы с сопротивлениями 10 Ом, 15 Ом и 20 Ом. Найдем общее сопротивление в параллельном соединении.
- Решение 1: Подставим значения сопротивлений в формулу:
1/Рпараллельное = 1/10 + 1/15 + 1/20
1/Рпараллельное = 3/30 + 2/30 + 1/30 = 6/30 = 1/5
Рпараллельное = 5 Ом
- Пример 2: В параллельное соединение подключены два резистора с сопротивлениями 8 Ом и 12 Ом. Найдем общее сопротивление в параллельном соединении.
- Решение 2: Подставим значения сопротивлений в формулу:
1/Рпараллельное = 1/8 + 1/12
1/Рпараллельное = 3/24 + 2/24 = 5/24
Рпараллельное = 24/5 = 4.8 Ом
Таким образом, общее сопротивление в параллельном соединении может быть определено путем сложения обратных величин сопротивлений, соединенных параллельно.
Пример 1: Вычисление сопротивления при двух параллельно соединенных резисторах
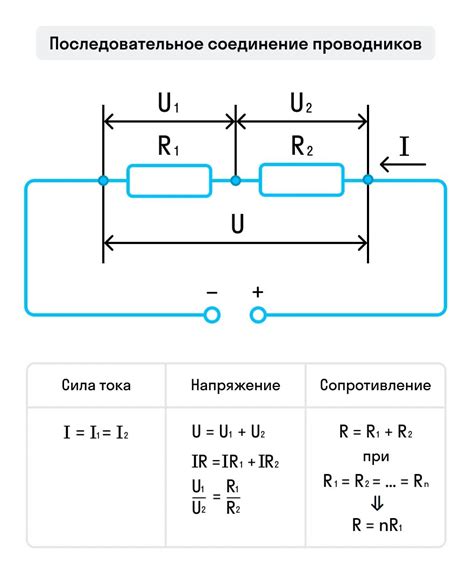
Допустим, у нас есть два резистора, сопротивление каждого из которых известно: R1 и R2. Мы хотим вычислить сопротивление общей схемы, когда эти два резистора соединены параллельно.
Формула для вычисления сопротивления параллельного соединения резисторов:
- Инвертируем значения сопротивлений каждого резистора: 1/R1 и 1/R2.
- Суммируем обратные значения: 1/Rобщ = 1/R1 + 1/R2.
- Инвертируем полученную сумму: Rобщ = 1/(1/R1 + 1/R2).
Теперь рассмотрим пример. Пусть у нас есть два резистора: R1 = 4 Ом и R2 = 6 Ом.
Вычислим сопротивление общей схемы:
- Инвертируем значения сопротивлений: 1/4 Ом = 0,25 Ом-1 и 1/6 Ом = 0,1667 Ом-1.
- Суммируем обратные значения: 0,25 Ом-1 + 0,1667 Ом-1 = 0,4167 Ом-1.
- Инвертируем полученную сумму: Rобщ = 1/(0,4167 Ом-1) = 2,4 Ом.
Таким образом, сопротивление общей схемы, состоящей из двух параллельно соединенных резисторов с сопротивлениями 4 Ом и 6 Ом, равно 2,4 Ом.
Пример 2: Вычисление сопротивления при нескольких параллельно соединенных резисторах
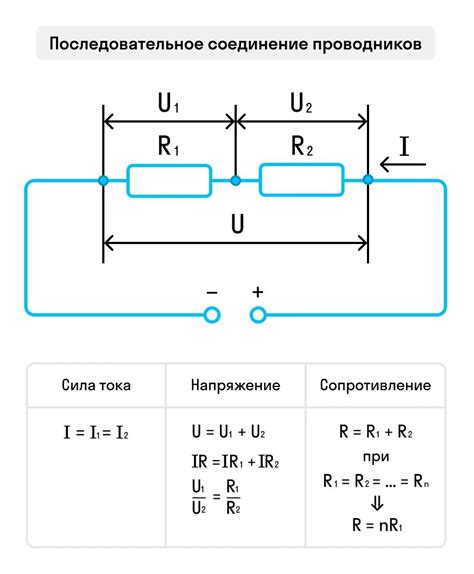
Допустим, у нас есть два резистора, R1 и R2, которые соединены параллельно.
Сопротивление резистора R1 составляет 4 Ом, а сопротивление резистора R2 - 6 Ом.
Чтобы найти общее сопротивление этой параллельной комбинации, мы можем воспользоваться следующей формулой:
1/Ртот = 1/Р1 + 1/Р2
Где Ртот - общее сопротивление, Р1 и Р2 - сопротивления каждого резистора.
Применяя эту формулу к нашему примеру, мы получаем:
1/Ртот = 1/4 + 1/6
Упростив выражение, мы получаем:
1/Ртот = 3/12 + 2/12 = 5/12
Для того чтобы найти общее сопротивление, нам нужно взять обратное значение от обеих сторон уравнения:
Ртот = 12/5 = 2.4 Ом
Таким образом, общее сопротивление параллельного соединения резисторов R1 и R2 равно 2.4 Ом.