Математика удивительна и полна интересных закономерностей. Одно из таких явлений – порядок операций в арифметических выражениях. Почему мы сначала умножаем, а потом складываем? Почему нельзя сделать наоборот? Разберемся в этом вместе!
Порядок операций в математике очень важен. Это связано с особенностями желаемых результатов и принципами самых базовых операций. Операции сложения и умножения обладают своими законами и свойствами.
Основной принцип умножения – свойство дистрибутивности. Оно заключается в том, что произведение одного числа на сумму двух чисел равно сумме произведений этого числа на каждое из двух чисел по отдельности. Такая особенность умножения позволяет нам применять его сначала к отдельным числам, а затем складывать полученные произведения. Именно поэтому мы сначала умножаем, а потом складываем.
Почему сначала умножение, а потом сложение?

Мы все знакомы с основными арифметическими операциями, такими как умножение и сложение. Но почему именно умножение выполняется перед сложением? Чтобы ответить на этот вопрос, нужно погрузиться в основы математики.
Умножение и сложение – две базовые операции в арифметике, которые используются для выполнения различных вычислений. Однако порядок выполнения этих операций имеет свое особое значение.
Порядок выполнения операций определяется по правилу математических операций, которое называется "порядок действий". Согласно этому правилу, умножение всегда выполняется перед сложением, если нет других указаний на обратный порядок.
Причина такого порядка заключается в том, что умножение обладает свойством дистрибутивности. Это означает, что умножение распространяется на сложение и делает его более компактным. Если бы порядок операций был обратным (сложение перед умножением), мы бы менее эффективно использовали свойства умножения.
Еще одна причина такого порядка операций – экономия времени и ресурсов. Умножение требует более сложных вычислений, чем сложение. Поэтому сначала выполняются сложение, которое легче и быстрее, а затем умножение для получения окончательного результата.
Иногда может возникнуть ситуация, когда необходимо поменять порядок выполнения операций. Для этого можно использовать скобки, которые задают определенный порядок вычислений.
Таким образом, порядок выполнения операций в математике основан на особых свойствах операций и экономическом обосновании. Сначала выполняется умножение, а затем сложение, чтобы облегчить вычисления и получить наиболее точный и эффективный результат.
Порядок математических операций
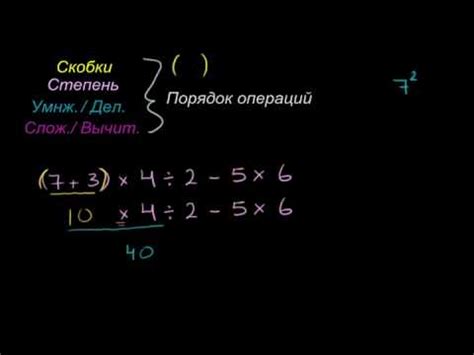
В математике существует установленный порядок приоритета операций, который следует при решении выражений:
- Скобки – сначала выполняются операции внутри скобок.
- Умножение и деление – затем выполняются операции умножения и деления, их порядок определяется слева направо.
- Сложение и вычитание – в конце выполняются операции сложения и вычитания, их порядок также определяется слева направо.
Этот порядок выполнения операций позволяет сохранять правильность и однозначность результата. Например, в выражении "2 + 3 * 4" сначала выполняется умножение (3 * 4 = 12), а затем сложение (2 + 12 = 14). Если бы порядок был другим, например, сначала выполнилось сложение (2 + 3 = 5), а затем умножение (5 * 4 = 20), результат был бы неверным.
Запомните и правильно применяйте правило порядка математических операций, чтобы выполнение сложных выражений было легким и точным!
Подробное объяснение приоритета операций
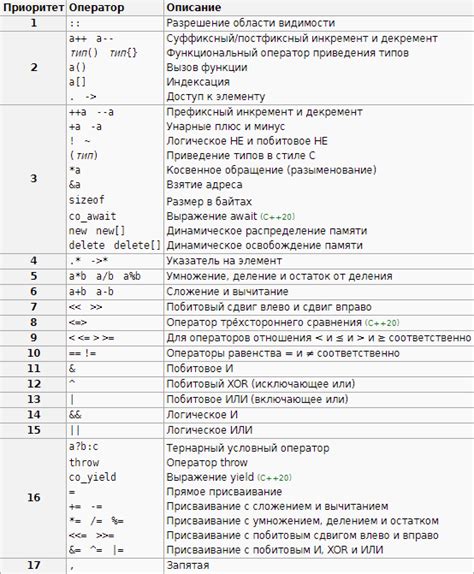
Зачем сначала умножение, а потом сложение? Это один из вопросов, который многие задают себе при изучении математики.
Приоритет операций в математике возникает из необходимости определить порядок выполнения различных операций в выражении. В общем случае, операции с более высоким приоритетом выполняются раньше операций с более низким приоритетом.
В математике существует установленная иерархия приоритетов операций, которая стандартизирована и применяется во всех математических выражениях. В этой иерархии операции с наивысшим приоритетом будут выполняться первыми, а операции с наименьшим приоритетом – последними.
Таким образом, умножение и деление обладают более высоким приоритетом, чем сложение и вычитание. Поэтому, при наличии умножения или деления в выражении, эти операции выполняются в первую очередь. А если в выражении нет умножения или деления, то сначала выполняются операции сложения и вычитания.
Для наглядности, в математике используют специальные символы, которые обозначают порядок операций и позволяют более ясно указать, какие операции должны выполняться раньше. Например, в выражении 2 + 3 * 4, символ "*", обозначающий умножение, указывает на то, что операцию умножения нужно выполнить раньше операции сложения. Поэтому, сначала происходит умножение 3 на 4, а затем сложение числа 2 с полученным результатом (12).
Важно помнить, что порядок выполнения операций можно изменить с помощью скобок. Если в выражении присутствуют скобки, то операции внутри скобок будут выполняться первыми, игнорируя стандартную иерархию приоритетов. Например, в выражении (2 + 3) * 4, скобки указывают, что сначала нужно выполнить операцию сложения (2 + 3), а затем умножения полученного результата на 4. Результат будет равен 20.
С помощью знания приоритетов операций можно более точно понимать, как работает математика и правильно выполнять вычисления. При этом важно помнить, что правила приоритета операций существуют для обеспечения единообразия и удобства в математических вычислениях.
Математические правила

Порядок выполнения операций – это соглашение о последовательности, в которой выполняются различные математические операции, такие как сложение, вычитание, умножение и деление. В общем принято считать, что умножение имеет более высокий приоритет, чем сложение.
Это объясняется тем, что умножение и деление – это операции более фундаментальные, чем сложение и вычитание. Умножение позволяет находить произведение двух чисел, а деление – находить отношение между ними. Сложение же и вычитание являются операциями, связанными с изменением числа или перемещением по числовой оси.
Если в выражении присутствуют и умножение, и сложение (или вычитание), то сначала выполняется умножение, а затем сложение или вычитание. Это правило называется равенством приоритетов. Например, в выражении 2 + 3 * 4 сначала выполняется умножение: 3 * 4 = 12, а затем сложение: 2 + 12 = 14.
Математические правила позволяют достичь правильных результатов при выполнении операций. Знание и соблюдение этих правил помогает точно решать математические задачи и облегчает работу с числами. Правило сначала умножение, а потом сложение – это лишь одно из множества правил, которые есть в математике. Изучая их, мы расширяем свои знания и умения в этой науке.
Примеры расчетов

Давайте рассмотрим несколько примеров, чтобы лучше понять, почему сначала выполняется умножение, а потом сложение.
Пример 1:
Рассмотрим выражение 2 + 3 * 4. Согласно порядку операций, умножение выполняется первым.
2 + 3 * 4 = 2 + 12 = 14
Таким образом, результатом данного выражения будет 14.
Пример 2:
Теперь рассмотрим выражение (2 + 3) * 4. Сначала выполняется операция в скобках.
(2 + 3) * 4 = 5 * 4 = 20
Таким образом, результатом данного выражения будет 20.
Пример 3:
Изучим выражение 2 * 3 + 4 * 5. Согласно порядку операций, сначала выполняется умножение, а затем сложение.
2 * 3 + 4 * 5 = 6 + 20 = 26
Таким образом, результатом данного выражения будет 26.
Это лишь несколько примеров, демонстрирующих принцип выполнения операций. Помните, что правильное понимание порядка операций помогает избежать ошибок в расчетах.
Особенности умножения и сложения

Умножение – это операция, которая увеличивает значение одного числа в несколько раз. Она осуществляется путем повторения сложения числа самого с собой определенное количество раз. Например, 2 умножить на 3 равно 2 + 2 + 2 = 6. Умножение обладает свойством коммутативности, то есть результат умножения двух чисел не зависит от порядка их записи. Кроме того, умножение обладает свойством ассоциативности, то есть результат умножения не зависит от способа расстановки скобок. Например, (2 умножить на 3) умножить на 4 равно 2 умножить на (3 умножить на 4).
Сложение – это операция, которая объединяет два числа в одно. Например, 2 плюс 3 равно 5. Сложение также обладает свойством коммутативности, то есть результат сложения двух чисел не зависит от порядка их записи. Кроме того, сложение обладает свойством ассоциативности, то есть результат сложения не зависит от способа расстановки скобок. Например, (2 плюс 3) плюс 4 равно 2 плюс (3 плюс 4).
Однако, умножение и сложение имеют и некоторые отличия. Например, результат умножения всегда больше или равен каждому из умножаемых чисел, а результат сложения может быть как больше, так и меньше слагаемых чисел. Кроме того, при умножении на 0 результат всегда будет равен 0, а при сложении со 0 результат будет равен другому слагаемому числу.
Понимание особенностей умножения и сложения позволяет нам эффективно использовать их в различных сферах нашей жизни, от решения математических задач до выполнения повседневных калькуляций.
Практическое применение

В бухгалтерии и налоговых сферах часто возникает необходимость умножать сумму налога на процент и затем добавлять результат к общей сумме. Например, если налог на товар составляет 10%, а его стоимость равна 1000 рублей, то после умножения налога на стоимость и сложения результата с исходной суммой мы получим итоговую стоимость.
Другой пример практического применения данного порядка операций - финансовый анализ. При анализе финансовых показателей часто необходимо учитывать не только сумму доходов, но и налоги, которые нужно учесть при подсчете фактической прибыли или рентабельности. Используя порядок умножения и сложения, мы можем правильно учесть налоги и получить точные результаты анализа.
Таким образом, знание правильного порядка операций в математике и его практическое применение помогает в решении разнообразных задач, связанных с налогами, финансовым анализом и другими сферами, где точность и правильность вычислений играют важную роль.