Математика - это наука, которая изучает законы и отношения между числами. Одним из важных понятий в математике является дробь, которая может быть представлена в виде числителя и знаменателя. Числитель - это число, которое стоит перед знаком деления, а знаменатель - это число, которое стоит после знака деления. Загадка числителя и знаменателя заключается в том, как они взаимодействуют друг с другом и каким образом можно проводить операции с дробями.
Числитель и знаменатель имеют различные функции. Числитель определяет количество частей, на которые нужно разделить целое число, а знаменатель определяет количество этих частей. Вместе они образуют дробь, которая позволяет представить часть целого числа.
Разумеется, в математике существуют определенные правила для работы с числителем и знаменателем. Например, можно складывать и вычитать дроби, умножать и делить их друг на друга. Это позволяет выполнять различные операции с дробями и решать математические задачи с их помощью.
Примерами использования числителя и знаменателя в математике могут служить задачи на расчет долей или процентов, а также на определение доли от общего количества. Например, если у нас есть 7 яблок, а мы хотим поделить их поровну между 2 друзьями, мы можем использовать дробь 7/2, где числитель будет равен 7 (общее количество яблок), а знаменатель - 2 (количество друзей). Таким образом, каждый друг получит 7/2 = 3,5 яблока.
Числитель и знаменатель в математике
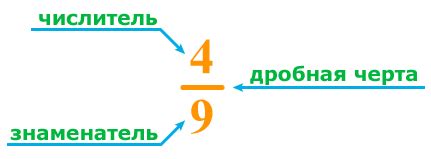
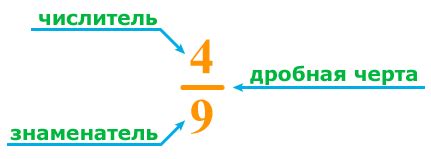
Числитель - это числовая часть дроби, обозначаемая числом, которое находится над чертой. Он показывает, сколько частей от целого мы рассматриваем или имеем в нашем расчете. Например, в дроби 3/5 числитель равен 3.
Знаменатель - это числовая часть дроби, обозначаемая числом, которое находится под чертой. Он показывает, на сколько частей целого мы делим или рассматриваем нашу дробь. Например, в дроби 3/5 знаменатель равен 5.
Числитель и знаменатель вместе образуют дробь и позволяют нам представлять и работать с частями от целого числа. Они определяют, какая часть целого мы рассматриваем и на сколько равных частей мы делим это целое. Благодаря этим понятиям мы можем выполнять операции сложения, вычитания, умножения и деления с дробями.
Значение и особенности числителя и знаменателя

Числитель обозначает количество частей дроби, которые мы берем, а знаменатель указывает, на сколько частей целое число разделено. Например, в дроби 3/4, числитель равен 3, что означает, что мы берем 3 части целого числа. Знаменатель равен 4, что означает, что целое число разделено на 4 равные части.
Числитель и знаменатель могут быть как положительными, так и отрицательными числами. Если числитель и знаменатель имеют одинаковый знак, то дробь называется положительной. Если числитель и знаменатель имеют разные знаки, то дробь называется отрицательной. Например, дроби -2/3 и 4/-5 являются отрицательными, а дроби 5/6 и -7/-8 являются положительными.
Кроме того, числитель и знаменатель могут быть как целыми, так и десятичными числами. В дроби 1/2, числитель равен 1, а знаменатель равен 2. В дроби 2.5/3, числитель равен 2.5, а знаменатель равен 3.
Значение числителя и знаменателя влияет на величину и характеристики дроби. Они определяют точность и показывают, сколько частей мы берем от целого числа. Например, если числитель больше знаменателя, то дробь больше 1 и называется неправильной дробью. Если числитель меньше знаменателя, то дробь меньше 1 и называется правильной дробью.
В итоге, числитель и знаменатель играют важную роль в представлении и интерпретации дробей. Они позволяют нам выразить доли, части и отношения между числами, и являются основными элементами математической дроби.
Примеры использования числителя и знаменателя

1. Обычная дробь:
Дробь 3/4 может быть представлена в виде числитель/знаменатель. Здесь 3 - числитель, а 4 - знаменатель.
2. Десятичная дробь:
Десятичная дробь 0.75 также может быть представлена в виде числителя/знаменателя. Здесь 75 - числитель, а 100 - знаменатель.
3. Проценты:
Проценты могут быть представлены в виде дроби, где числитель - это значение процента, а знаменатель - 100. Например, 50% эквивалентно дроби 50/100.
4. Мнимая единица:
В комплексных числах используется мнимая единица "i", которая равна квадратному корню из -1. Здесь числитель может быть записан в виде i, а знаменатель - 1. Например, в форме дроби i/1.
5. Уравнения:
При решении уравнений или систем уравнений, числители и знаменатели используются для обозначения отношений между различными параметрами или переменными.
6. Графики:
На графиках числитель и знаменатель используются для определения наклона, пересечения с осями и других свойств функций или уравнений.
Использование числителя и знаменателя является основным элементом для понимания и работы с рациональными числами в математике. Понимание и применение этих понятий помогают в решении различных проблем и задач, которые связаны с дробями, процентами, комплексными числами и другими математическими концепциями.
Понятие числителя и знаменателя в дробях

Числитель обозначает количество частей, на которое разделено целое число или объект, а знаменатель указывает на общее количество этих частей или на единицу измерения. Например, в дроби 3/4 - числитель равен 3, что означает, что имеется 3 части из общего количества равного 4.
Числитель и знаменатель могут быть положительными, отрицательными или нулями. Отрицательный числитель или знаменатель указывает на отрицательное значение дроби, а ноль в числителе или знаменателе говорит о том, что дробь равна нулю.
В зависимости от значения числителя и знаменателя, дроби могут быть эквивалентными или неэквивалентными. Если две дроби имеют одинаковое отношение числителя к знаменателю, они называются эквивалентными. Например, дроби 3/4 и 9/12 являются эквивалентными, так как обе дроби имеют одинаковое отношение 3 к 4.
Понимание значений числителя и знаменателя позволяет проводить различные операции с дробями, такие как сложение, вычитание, умножение и деление. Знание этих понятий не только облегчает работу с дробями, но и является важной основой для изучения более сложных математических концепций.
Числитель и знаменатель в пропорциях
Числитель в пропорции играет важную роль, так как он определяет количество раз, когда одно значение содержится в другом. Он помогает определить отношение между двумя числовыми значениями.
Знаменатель в пропорции также имеет свою важность. Он определяет единицы измерения или контекст, в котором происходит сравнение между двумя значениями. Знаменатель позволяет понять, какое значение является базовым или сравнительным.
Пропорции могут встречаться в различных ситуациях и областях, таких как финансы, геометрия и технические науки. Например, пропорции могут использоваться для расчета коэффициентов пропорциональности в экономике или определения соотношения между сторонами геометрической фигуры.
Важно понимать и использовать числитель и знаменатель в пропорциях для правильного анализа и решения математических задач и проблем. Понимание их роли и значения помогает в сравнении и изучении различных значений и их отношений.



