Геометрия, как наука, изучает основные фигуры, их свойства и взаимосвязи. Одной из основных фигур в геометрии является окружность. Окружность представляет собой множество точек, равноудаленных от данной точки, которая называется центром окружности. Важным понятием в геометрии окружности является хорда центрального угла.
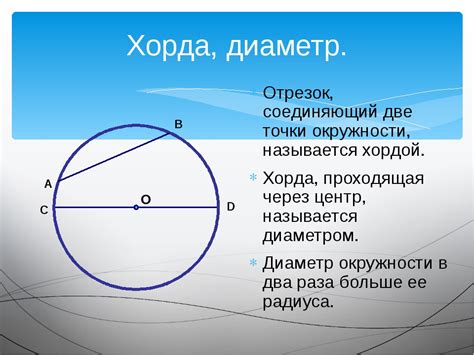
Хорда центрального угла – это отрезок, соединяющий две точки на окружности, которые лежат на одном измерении угла с центром в этой окружности. Центральный угол определяется как угол, образованный двумя лучами, исходящими из центра окружности и проходящими через две точки на окружности.
Хорда центрального угла играет важную роль в геометрии и находит применение в различных задачах и теоремах. Например, между хордой центрального угла и измерением этого угла существует простая связь. Если угол составляет 180 градусов, то хорда является диаметром окружности. Если угол меньше 180 градусов, то хорда является отрезком, не проходящим через центр окружности.
Таким образом, понимание хорды центрального угла является важным аспектом геометрических вычислений и позволяет решать различные задачи, связанные с окружностями. Знание этого понятия поможет более глубоко понять и осмыслить свойства и взаимосвязи между фигурами в геометрии.
Что такое хорда центрального угла?
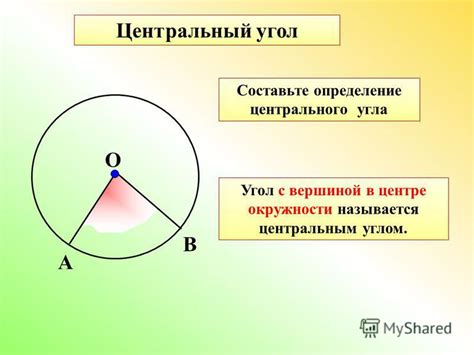
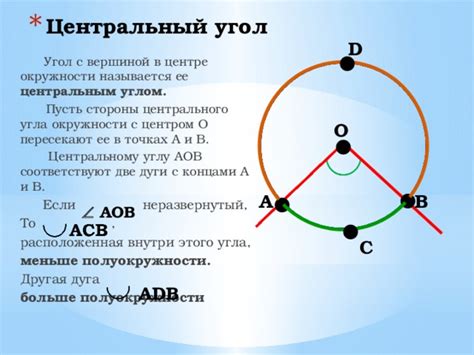
Хорда центрального угла играет важную роль в геометрии. Она является основным элементом для определения центрального угла - угла, его вершиной является центр окружности, а сторонами являются радиусы, исходящие из центра к концам хорды. Центральный угол также равен двойному углу, образованному хордой.
Хорды центрального угла используются для изучения свойств окружности и ее взаимосвязей с другими фигурами. Они могут быть использованы для нахождения длины хорды, а также для определения других геометрических характеристик окружностей, таких как длина дуги или площадь сектора.
Важно отметить, что хорда центрального угла может быть любой длины, включая диаметр окружности, который является самой длинной хордой. Кроме того, чем ближе концы хорды к друг другу, тем меньше будет центральный угол.
Определение хорды центрального угла
Хорда центрального угла обладает несколькими свойствами:
- Длина хорды центрального угла меньше или равна диаметру окружности;
- Длина хорды центрального угла не зависит от положения точек на окружности;
- Если две хорды центрального угла имеют одинаковую длину, то они равны друг другу.
Хорды центральных углов широко используются в геометрии для нахождения различных геометрических отношений и решения задач.
Свойства хорды центрального угла
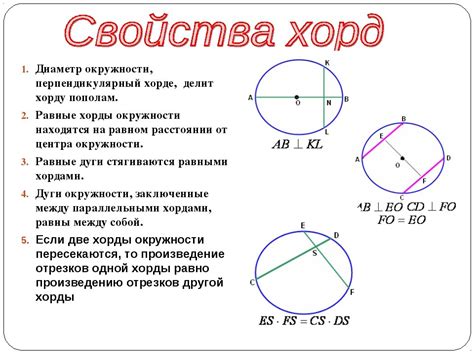
1. Длина хорды центрального угла
Длина хорды центрального угла зависит от радиуса окружности и величины данного угла. Для определения длины хорды можно использовать соотношение:
Длина хорды = 2 * радиус * sin(α/2)
где α - величина центрального угла, радиус - расстояние от центра окружности до хорды.
2. Получение угла, заключенного между хордой и дугой окружности
Если известны длина хорды и радиус окружности, можно вычислить величину угла между хордой и дугой, образуемой этой хордой. Для этого можно использовать формулу:
α = 2 * arcsin(длина хорды / (2 * радиус))
где α - величина угла между хордой и дугой, радиус - расстояние от центра окружности до хорды.
3. Угол, образованный двумя пересекающимися хордами
Если две хорды пересекаются на окружности, то угол, образованный этими хордами в точке их пересечения, равен половине суммы мер дуг на окружности, которые заключены между этими хордами.
Применение хорды центрального угла
В геодезии хорда центрального угла используется для измерения расстояний на поверхности Земли. Подобно радиусу, который определяет положение точек на окружности, хорда центрального угла помогает определить расстояние между двумя точками на поверхности.
В конструировании и архитектуре хорда центрального угла используется для построения дуг и круговых конструкций. Она позволяет определить форму и размер дуги, а также установить точки пересечения, что является важным при создании эстетически приятных и функциональных конструкций.
Кроме того, хорда центрального угла может использоваться для решения различных математических задач, связанных с геометрией. Она помогает определить углы, длины отрезков и другие геометрические параметры.
В итоге, хорда центрального угла - важный элемент геометрии, который находит широкое применение в различных областях. Она помогает измерять расстояния, строить дуги и круговые конструкции, а также решать математические задачи.
Практическое использование хорды центрального угла

Одним из практических применений хорды центрального угла является использование ее в астрономии. Например, в навигации по морю и воздуху для определения местоположения путем измерения углов между наблюдателем и звездами. Хорда центрального угла используется в этом случае для определения угла между небесными объектами и горизонтом. Эта информация затем используется для вычисления координат местоположения наблюдателя.
В инженерии хорда центрального угла используется для определения расстояний и размеров объектов на основе их изображений. Например, при проектировании дорожных сетей или крупных строительных объектов, используется метод определения дальности по изображению объекта и хорде центрального угла.
В дизайне хорда центрального угла используется для создания гармоничных композиций и расстановки объектов. Например, при разработке логотипов или дизайна упаковки, дизайнеры часто используют хорду центрального угла для создания балансированного и привлекательного визуального впечатления.
Таким образом, практическое использование хорды центрального угла широко разнообразно и находит применение в различных областях. Благодаря своей геометрической природе, хорда центрального угла является универсальным инструментом для измерений и расчетов, а также для создания эстетически приятных композиций и дизайнов.