Средние значения являются одним из основных понятий в статистике. Они позволяют суммировать и анализировать данные, чтобы получить общую информацию о наборе чисел или значений. Существует несколько различных типов средних, каждое из которых имеет свое значение и применение.
Выборочное среднее (среднее арифметическое) является наиболее распространенным типом среднего значения. Оно вычисляется путем сложения всех значений в выборке и деления полученной суммы на количество значений. Выборочное среднее показывает среднее значение, которое можно ожидать от случайно выбранного элемента из выборки. Оно часто используется для измерения центральной тенденции данных.
Арифметическое среднее является дополнительным типом среднего значения, который используется в статистике. В отличие от выборочного среднего, арифметическое среднее вычисляется путем усреднения значений из различных выборок. Это может быть полезно, когда нужно объединить данные из нескольких источников для получения общего представления о целевой группе. Арифметическое среднее также может быть использовано для определения суммарной статистики по группе.
Геометрическое среднее является еще одним типом среднего значения и используется для измерения относительных изменений величин или процентных изменений. Оно вычисляется путем перемножения всех значений в выборке и извлечения корня из произведения по количеству значений. Геометрическое среднее проявляет свойства логарифма, что позволяет использовать его для учета процентных изменений внутри выборки.
Значение различных типов средних

Арифметическое среднее также известно как среднее значение или среднее арифметическое. Оно вычисляется как сумма всех значений в выборке, деленная на количество этих значений. Арифметическое среднее также является хорошей мерой центральной тенденции и позволяет получить представление о среднем значении в выборке.
Геометрическое среднее является другим типом среднего значения. Оно вычисляется как корень n-ной степени из произведения всех значений в выборке, где n - количество значений в выборке. Геометрическое среднее полезно в случаях, когда значения в выборке связаны между собой множественными процентными изменениями, так как оно усредняет процентные изменения величин.
Знание различных типов средних позволяет получить более полное представление о данных и использовать разные подходы к анализу. Выборочное среднее и арифметическое среднее часто используются для оценки средних значений, в то время как геометрическое среднее может быть полезно при работе с процентными изменениями. Важно помнить, что выбор типа среднего зависит от контекста и целей анализа.
Средние значения: выборка, арифметическое, геометрическое
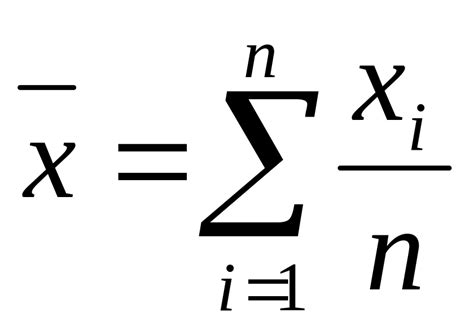
Выборочное среднее является наиболее распространенным типом среднего значения. Оно рассчитывается путем суммирования всех значений в выборке и деления на количество элементов в выборке. Выборочное среднее является хорошим представлением среднего значения, особенно когда выборка хорошо отражает данные.
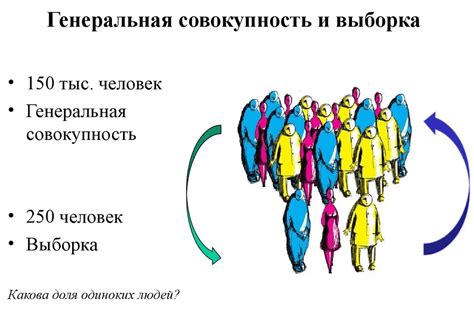
Арифметическое среднее также является широко используемым типом среднего значения. Оно рассчитывается также, как и выборочное среднее, но на этот раз применяется ко всей генеральной совокупности. Арифметическое среднее является полезным показателем в случае, когда доступны все данные популяции или генеральной совокупности.
Геометрическое среднее является менее распространенным типом среднего значения, но может быть полезным в определенных случаях. Оно рассчитывается путем извлечения корня из произведения всех значений в выборке. Геометрическое среднее особенно полезно, когда данные имеют экспоненциальный рост или спад, такие как процентные изменения или степени.
Каждый из указанных типов среднего значения имеет свои особенности и применение в статистике. Выбор правильного типа среднего значения зависит от конкретной задачи, данных и цели исследования. Важно учитывать контекст и обстоятельства, чтобы получить наилучший результат и наиболее точную оценку центральной тенденции данных.
Выборка: понятие, применение, особенности
| Особенности выборки |
|---|
| 1. Репрезентативность |
| Выборка должна быть репрезентативной, то есть адекватно отражать свойства генеральной совокупности. Для этого необходима правильная и случайная выборка, чтобы исключить возможные искажения и ошибки. |
| 2. Размер выборки |
| Размер выборки должен быть достаточным для получения статистически значимых результатов. Оптимальный размер выборки зависит от множества факторов, таких как размер генеральной совокупности, допустимая погрешность и статистические методы анализа. |
| 3. Методы исследования |
Арифметическое среднее: определение, расчет, применение

Для расчета арифметического среднего необходимо выполнить следующие шаги:
- Сложите все числа в выборке
- Поделите полученную сумму на количество элементов в выборке
Применение арифметического среднего может быть разнообразным:
- Определение среднего значения величины. Например, при измерении температуры в разных днях можно использовать арифметическое среднее для нахождения средней температуры за определенный период.
- Сравнение различных групп данных. Например, при анализе результатов эксперимента можно сравнить средние значения полученные в контрольной и экспериментальной группах.
- Прогнозирование будущих значений. Например, при анализе истории торговых цен можно использовать арифметическое среднее для предсказания будущих цен на товары или акции.
Арифметическое среднее является полезным инструментом для обработки числовых данных, позволяющим получить информацию о среднем значении выборки. Используя арифметическое среднее, можно проводить сравнения, анализировать данные и делать прогнозы.
Геометрическое среднее: суть, использование, особенности

Суть геометрического среднего заключается в следующем: для ряда чисел необходимо взять их произведение, а затем извлечь из него корень с указанным порядком, где порядок равен количеству сомножителей. Полученное значение и будет являться геометрическим средним.
Геометрическое среднее часто применяется при работе с процентными изменениями, где требуется учесть непропорциональное соотношение между увеличением и уменьшением.
Особенностью геометрического среднего является его свойство неустойчивости к экстремальным значениям. Даже при наличии одного единственного значения, которое сильно отличается от других, геометрическое среднее будет приближаться к этому экстремальному значению.
Геометрическое среднее также используется в различных областях, таких как финансы, экономика, статистика и биология.